Is it secure to transmit a short plaintext with its MAC?

Question

I have a short (32-bit) message that needs to be authenticated. Due to the constraints of my platform, I would like to use Speck32/64 (32-bit block, 64-bit key) with a Matyas-Meyer-Oseas one-way compression function (due to its ease of implementation and because the input sizes match what Speck generates).

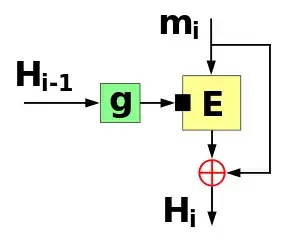
(Here, $E$ is Speck32/64, $g$ is a no-op, $m_i$ is the entire short message, $H_i$ is the tag, and $H_{i-1}=H_0$ is secret.)

However, my message is short enough that there won't be more than one iteration of the compression function; essentially, I would merely be XORing the output of the cipher with the plaintext. (Obviously, $H_0$ should remain secret!) I also don't care about the secrecy of the message, only its unforgability. Therefore, I would transmit the message in plaintext along with its equally-sized MAC.

Is it secure to give a third party the plain text that goes with a MAC? In other words, does the fact that the third party always knows the plaintext to a given tag weaken the security of the tag? If so, what needs to be changed to secure the message?

Answer 1

A normal security notion for MAC's is that of unforgeability. So given some set of message,tag pairs $(m_0,t_0),\ldots,(m_k,t_k)$ is should be hard to create a tag for a new message not among the $\{m_0,\ldots,m_k\}$, stated informally.

In your case, you could just use $E_k(m_0)$ with the secret MAC key $k$ ($H_0$ in your notation); no need for the extra XOR (it does nothing for security; you know $m_0$ anyway, so we might as well use $E_k(m_0)$). This is just a standard use of a keyed random function (which we will suppose a block cipher is) as a MAC for short messages. It's construction 4.5 on page 117 in Katz and Lindell (second edition) book "an introduction to modern cryptography", which also has the (short) security proof for this construction for the above notion of security.

You do realise that your construction does allow for replay attacks, I suppose?