I explain, criticize and try to improve the technique in the question (which asks for speed by using cryptographic techniques for arguably satisfactory functionality in a statistical simulation). Shuffling, and full-blown Format-Preserving Encryption aim at perfect or demonstrable cryptographic security, a different goal.
Under the assumption that the (unstated) distribution of the entries to compute is rather arbitrary, and storing $J\cdot N\cdot\lceil\log_2(N)\rceil$ bits is not a viable option, the general technique in the question seems best: build an efficient keyed pseudo-random permutation $P$ of the set $\{0\dots N-1\}$, with the key (noted $y$ to prevent a clash in notation) random, or obtained from the permutation index $j\in\{0\dots J-1\}$ (e.g. as $y=y_0\oplus j$ with $y_0$ a random constant fixed at the beginning of the many iterations); then evaluate $P_y(x)$ as needed.
The question builds $P$ from a block cipher $E$ of $n=\lceil\log_2(N)\rceil$-bit block size, with $P_y(x)$ computed by the cycle-walking technique:
- repeat
- until $x<N$
- output $x$
Any $P_y$ demonstrably is a permutation of the set $\{0\dots N-1\}$. $P$ is demonstrably at least as secure as $E$ is (ignoring side-channel issues, e.g. by timing or power analysis). Computing $P_y(x)$ uses on average $2^n/N<2$ evaluations of $E$, and at most $2^n-N+1<N$.
The question builds $E$ as a Feistel cipher, symmetric if $n$ is even, or mostly so if $n$ is not. It has 4 rounds of an ad-hoc round function, based on truncated AES S-boxes (see details in comments to the present questions), without gapping flaw that I could spot for $n\approx13$.
Even with a good design per the description given, there are potential issues: the Luby-Rackoff result (How to Construct Pseudo-random Permutations from Pseudo-random Functions, in proceedings of Crypto 1985) ensuring security for a Feistel cipher after 3 rounds (4 if we consider adaptive chosen ciphertext attacks) is only valid for independent and random round functions; asymptotically when $n$ grows; and when the number of distinct inputs evaluated is much less than $2^{n/2}$ (here, $\sqrt N$), something which is not warranted in the application. More rounds are needed as more space is explored (see Jacques Patarin's Luby-Rackoff: 7 Rounds Are Enough for $2^{n(1−\epsilon)}$ Security, in proceedings of Crypto 2003).
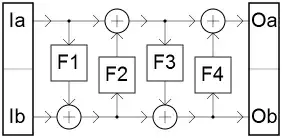
Expanded: I'll show why with small width of $E$, we need more than 4 rounds for something even approaching cryptographic soundness. In a 4-rounds symmetric Feistel cipher as illustrated above, if two keyings use identical $F_2$ within XOR of a constant at input, and identical $F_3$, then for any $I_a$, the function $I_b\to O_b$ is identical within XOR of a constant (dependent on $I_a$) at input. This characteristic is improbable to the utmost for two sizable random permutations (odds about $2^{n(2^{n/2-1}-2^{n-1})}$, that is $2^{-24192}$ for $n=12$), and should it occur is easily detectable and conceivably could have an impact on a practical application. In the construction considered (detailed in comments to this question) for $n=12$, each round function is XOR with a 6-bit constant followed by one in $2^8$ S-boxes of 6x6 bits, thus any two random keyings have $F_2$ and $F_3$ causing that characteristic with odds $2^{-22}$, and this is expected to occur over a hundred times among $J=25000$ permutations constructed as proposed. For a practical attack, we choose an arbitrary fixed $I_a$, and partially map $I_b\to O_b$ for random $I_b$ (a little more than $2^{n/4}$ evaluations for each of the $J$ permutations will do); when we find a collision $E_b(I_a\|I_b)=E_b'(I_a\|I_b')$, we check if $\forall x,E_b(I_a\|(I_b\oplus x))=E_b'(I_a\|(I_b'\oplus x))$ (in the affirmative, we can then confirm that a similar property holds for any other $I_a$, and it is practically certain that $E$ and $E'$ share the same S-boxes in $F_2$, and in $F_3$, and the same XOR constant on entry of $F_3$). It is overwhelmingly likely that we will find a pair $(E,E')$ with such property when using the construction proposed in the question, and practically impossible for random permutations. The attack can be adapted to work for $P$ built using cycle-walking.
Corrected: Also, we can imagine applications where parity of permutation $P$ could have an impact, such as distribution of the number of swaps in sorting. Any Feistel cipher yields an even permutation, thus $E$ is even. While $N<2^n$ allows $P$ to be either even or odd, its parity will we strongly biased for many values of $N$ (argument: when $2^n-N$ is small compared to $\sqrt N$, for most $E$, the cycle-walking repeat loop is executed exactly twice for $2^n-N$ inputs, and once for all the others, so that the resulting parity of $P$ is $N\bmod 2$). So we need an ample amount of cycle-walking (this other question asks how much), or making the permutation even or odd under control of a key bit (a simple technique uses XOR of any ciphertext that is all-zero except its rightmost bit, with a key bit controlling parity), or deviating from straight Feistel (like, using modular addition instead of XOR to combine the round function's result with the half state).
More generally: A recommendable way to inject entropy in a Feistel construct of small width is to use modular addition of a round key over the whole state width (rather than XOR over half the state as in the question's Feistel construct): that injects nearly twice as much entropy, which is very desirable; and balances the permutation's parity.
With careful specification of the Feistel cipher using somewhat more rounds, more key material injected, and dealing with the parity issue (except when clearly immaterial, which includes any case where at least 2 inputs are never used), the method has merit. The idea in another answer of using AES-NI instructions to build the round function would give something very fast, but at the expense of portability, and I will not venture into this.
Here is a revised tentative, christened fastperm2, to use cryptographic techniques in order to build efficient random permutations over a small domain. I stress that I give no insurance of cryptographic security; still, I challenge one to find an attack in the random key setup much better than $2^{64-i}$ steps for odds $2^{-i}$ of success, even restricted to a particular $N$.
Rationale:
- easy to code in C;
- limited amount of cycle-walking, for the extra effort is better spent on more rounds;
- minimally simple round function, without S-boxes, using:
- diffusion (to the left, and to some limited degree to the right) by modular multiplication with a public multiplier;
- right diffusion and non-linearity by XOR with right-shifted state;
- combination with round keys using addition over the full state, to maximize key material and deal with permutation parity;
- at least 16 rounds in hope to compensate for that simplicity (I wish I could justify that value other than by analogy with serious ciphers).
- enough rounds that at least 64 bits of entropy are injected in each half of the cipher discarding one round (for hoped 64-bit security against a generic meet-in-the-middle attack);
- restrict domain so that $N!$ is comfortably above $2^{128}$, and state fits a 32-bit word.
Parameter selection according to $N$:
- ensure $40\le N\le 2^{32}-2^{20}$ (for lower $N$, nothing beats Fisher-Yates anyway);
- find the lowest $M$ with $N\le M$ such that $M\equiv2^k\pmod{2^{k+1}}$ with $k$ the integer closest to $n(\sqrt5-1)/2)$ where $n=\lceil\log_2(M)\rceil$ (thus: $6\le n\le32$, $k=\lfloor(13n+10)/21\rfloor$, and $M=(2\big\lfloor\lceil N/{2^k}\rceil/2\big\rfloor+1)2^k$);
- $r\gets2\max(\lceil64/(n-1)\rceil+1,8)$, the number of rounds.
- $C\gets\lfloor(28657M+23184)/46368/2^k\rfloor2^k+(\text{7D8B5}_{16}\bmod 2^k)$ (so that $C\approx M(\sqrt5-1)/2$, and the low $k$ bits of $C$ are per the constant $F_{29}\equiv5\bmod 8$);
- while $\gcd(C,M)\ne1$
- $s\gets n-k$, the shift count;
Note: parameters are such that $x\to C\cdot x\bmod M$ and $x\to x\oplus\lfloor x/2^s\rfloor$ are permutations of the set $\{0\dots M-1\}$. The first transformation achieves good left diffusion in the state bits; both transformations give some right diffusion (though limited to the leftmost $s$ bits for the first transformation).
Sub-keys setup:
- for each $j$ with $0\le j<r$
- set $y_j$ to a uniformly random value in $\{0\dots M-1\}$ (or using an unspecified pseudo-random function of $y$ and $j$)
Encryption of $x$ with $0\le x<N$:
- repeat
- for each $j$ with $0\le j<r$ in ascending order
- $x\gets(C(x\oplus\lfloor x/2^s\rfloor)+y_j)\bmod M$
- while $x\ge N$
- output $x$
It is critical that multiplication and modular reduction is implemented exactly. In C99 and assuming all variables are of type uint32_t, a round is:
x = ((x ^ x>>s)*(uint64_t)C + y[j]) % M;
Plan: give a reference C implementation.
For a statistical application, the number of rounds $r$ can be lowered; I conjecture that $r\gets2\max(\lceil40/(n-1)\rceil+1,5)$ would pass any randomness test not constructed with knowledge of the cipher's structure, including any pre-existing test.
Revisions: Two awful typos in the round function have been fixed. I am back to considering that $n-1$ bits of entropy are injected per round (rather than $k$ in the short-lived fastperm3). Upped the entropy injected in the reduced version for statistical use, in order to lower the odds of near-identical permutations..
