Proving the possession of signature in zero-knowledge

Question

Does anybody know an efficient mechanism to prove the possession of a digital signature (e.g. RSA) on a certain attribute (message) in zero-knowledge? That is, without revealing the actual signature (against tracking, for privacy) prove that you have one? Thanks a lot in advance!

Answer 1

Guillou and Quisquater (link) present a zero-knowledge proof of an RSA signature. Basically, the scheme is as follows:

Public knowledge: RSA modulus $n$, public RSA exponent $v$, preimage $X$.

Secret knowledge for prover: $A$, such that $A^v = X \mod n$.

$$ \begin{matrix} \mathcal{P} & & \mathcal{V} \\ r \xleftarrow{\$} \mathbb{Z}_n^* \phantom{\mod n} & & \\ T \leftarrow r^v \mod n & & \\ & \xrightarrow{\quad{}T\quad{}} & \\ & & d \xleftarrow{\$} \{0,1,\ldots,v-1\} \\ & \xleftarrow{d} & \\ t \leftarrow A^dr \mod n & & \\ & \xrightarrow{\quad{}t\quad} & \\ & & t^v \stackrel{?}{=} X^{d}T \mod n \end{matrix} $$

In this diagram, $\leftarrow$ denotes assignment of a value to a variable and $\xleftarrow{\$}$ denotes uniformly random selection from a finite set.

Answer 2

For many signature schemes based on zero knowledge proofs of discrete log knowledge, (EG:Schnorr signature, ECDSA) it is possible to perform an interactive proof that a signature exists without revealing the signature. This proof is interactive only, and a dishonest verifier cannot turn it into a non-interactive proof.

A Schnorr signature for a public key Y=xG (x is secret key) is a tuple (e,s) such that for an R R=eY+sG, e=H(R,m). Where H is a cryptographic hash.

It is verified by computing R=eY+sG from the (e,s) signature tuple, then checking that e=H(R,m) holds.

Suppose Alice has a signature on a string m and wishes to prove that a signature (e,s) exists to Bob. Alice first sends everything but the s scalar.

• A-->B:(m,R)
• Bob: compute e=H(R,m),S=R-e*Y

Bob can, with R and m compute the point S in the equation for the valid signature but not the discrete log s of that point. If Bob could do that he could sign things.

Alice does know the scalar s and can prove this by using it as a key during a Diffie-Hellman key exchange. DH acting as an interactive only proof.

• Bob: generate ephemeral public key Y_b=b*G
• B-->A: Y_b
• Alice: compute K=Y_b*s,
• A-->B: H(K,context)
• Bob: compute K=b*S, verify H(K,context)=(received_value)

Alice has proven knowledge of the scalar s in the signature (e,s) tuple without revealing it to Bob. DH key exchange shouldn't reveal anything about s especially with that hash in there to destroy any algebraic structure.

Note that there are a lot of extra back and forth steps in the protocol above. If Bob has a known public key, Alice can just send Bob (e,H(K,context),context,m) or (R,H(K,context),context,m), with Bob computing S and verifying H(K,context). Bob can provide an ephemeral challenge key as a first step if there's no such widely known key.

Sending K directly may be fine, although it makes Alice into a "multiply by s oracle". The context helps if using Bob's public key since Eve the eavesdropper who listens in on the exchange doesn't learn K and so can't compute the hash value for a different (proverID,verifierID,time) context, preventing replay attacks.

---

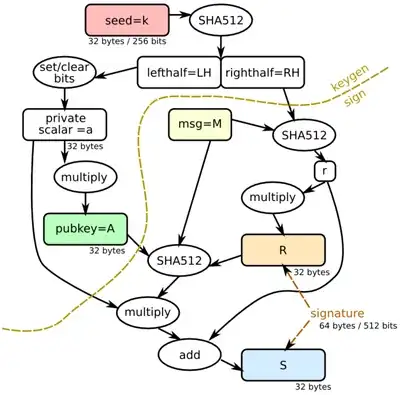
The following python code uses the NACL library to generate signatures. Additionally the ECPy library is used to implement EC calculations concisely. You can use NACL._sodium.(whatever) but that's a lot more verbose. AFAIK this should just work securely assuming you have an ED25519 signature. Vanilla Schnorr signatures require slight changes to a few sections.

The following graphical overview of the ED25519 signature system is useful for understanding the code below.

from nacl.signing import SigningKey
import json
gov_sk=SigningKey(b"1"*32)
gov_pk=gov_sk.verify_key.encode()
alice_ID={"info":json.dumps(
    {"name":"Alice Liddell",
     "DOB":"1970-01-01",
     "occupation":"cryptographer"}).encode("utf8")}
alice_ID["sig"]=gov_sk.sign(alice_ID["info"])[:64]
from ecpy.curves import Curve
cv = Curve.get_curve('Ed25519')
import hashlib
def decodeint(s):
    return sum(256*i  b for i,b in enumerate(bytearray(s)))
def encodeint(y,n):
    return bytes(bytearray((y>>i*8)&255 for i in range(n)))
def sha512(m):return hashlib.sha512(m).digest()
def h_int(m):return decodeint(sha512(m))
def verify(sig,pk,m):
    #verify an ed25519 signature
    assert len(sig)==64
    R = cv.decode_point(sig[0:32])
    A = cv.decode_point(pk)
    s = decodeint(sig[32:])
    h = h_int(cv.encode_point(R) + pk + m)
    return cv.generators == R+Ah
#check the signature
if verify(alice_ID["sig"],gov_pk,alice_ID["info"]):
    print("Alice verified she has a valid signature")
def get_sk_scalar(sk):
    return cv.decode_scalar_25519(sha512(sk.encode())[:32])
def make_proof(sig,challenge_key,m,context=b""):
    R=sig[0:32]
    PKc = cv.decode_point(challenge_key)
    s = decodeint(sig[32:])
    K = cv.encode_point(s * PKc)
    H = sha512(K+context)[:32]
    proof = R+H+encodeint(len(context), 2)+context+m
    return proof
def check_proof(proof,challenge_sk,pk):
    #unpack
    def get(n,i=[0]):
        data=proof[i[0]:i[0]+n] if n>=0 else proof[i[0]:];i[0]+=len(data)
        if len(data)<n:raise ValueError("not enough data")
        return data
    R = cv.decode_point(get(32))
    H = get(32)
    context=get(decodeint(get(2)))
    m = get(-1)#remainder
#calculate S from signature equation
A = cv.decode_point(pk)
h = h_int(cv.encode_point(R) + pk + m)
S = R+A*h
#check the DH shared key sha512 was correctly calculated
K=cv.encode_point( S * get_sk_scalar(challenge_sk))
H_target=sha512(K+context)[:32]
if H_target!=H:
    raise Exception(&quot;verification failed&quot;)
return context,m


#bob has a known key or generates an ephemeral challenge key for the protocol.
bob_sk=SigningKey((b"bob"*100)[:32])
bob_pk=bob_sk.verify_key.encode()
print("Bob --> Alice: challenge key:",repr(bob_pk))
#Alice makes a proof
proof=make_proof(sig=alice_ID["sig"], challenge_key=bob_pk, m=alice_ID["info"],
                 context=json.dumps({"prover":"Alice","verifier":"Bob","date":"2023-01-01T01:02:59Z"}).encode())
print("Alice --> Bob: proof:",repr(proof))
#bob can verify it
result=check_proof(proof, bob_sk, gov_pk)
print("Bob knows the following was signed:",result[1])
print("with protocol context:",result[0])

This should work for signatures based on discrete log problems. Schnorr makes the transformation clean. ECDSA is messier. Alice can prove knowledge of dlog(R) in base (H(m)*G+r*Q_A) (IE:factor inverse(S) out of the right side of the R=(H(m)/s)*G+(r/s)*Q_A equation. Bob chooses an ephemeral key with (H(m)*G+r*Q_A) as the generator and they do DH as above. There are also ways to use trapdoor one way functions to do non-interactive zero knowledge proofs that can either be generated legitimately or forged by using the trapdoor (Bob's secret key) to mess with the output of the random oracle. The resulting proof will convince Bob (and only Bob) that the signature exists.

Answer 3

One-Way Aggregate Signatures (OWAS) (also called composite signatures) can be used to do this. They are based on BLS signatures. I will skip the notation except mention that they are based on bilinear pairings. The above links will give the details.

Let $H$ be a hash function and $x_1$ be the private key. The public key is $y_1=g^{x_1}$. For any message $m_1$, the signature is $\sigma_1={h_1}^{x_1}$, where $h_1 = H(m_1)$. To verify the signature, test that: $\hat{e}(\sigma_1, g) \stackrel{?}{=} \hat{e}(h_1, y_1)$ holds.

Let $x_2$ be another private key. The public key is $y_2=g^{x_2}$. As before, for any message $m_2$, the signature is $\sigma_2={h_2}^{x_2}$, where $h_2 = H(m_2)$. To verify the signature, test that: $\hat{e}(\sigma_2, g) \stackrel{?}{=} \hat{e}(h_2, y_2)$ holds.

We can also combine $\sigma_1, \sigma_2$ into an aggregate signature $\sigma$ as follows: $\sigma=\sigma_{1}\cdot \sigma_{2}$. To verify, we check that: $$\hat{e}(\sigma, g) \stackrel{?}{=} \hat{e}(h_1, y_1)\cdot\hat{e}(h_2, y_2)$$

The signatures satisfy the standard security as shown in the Aggregate Signatures Paper. That is, assuming that the Diffie-Hellman problem is hard, presentation of $\sigma$ proves that $y_1$ signed $m_1$ and $y_2$ signed $m_2$ (even if the original signatures are not provided).

The security of OWAS relies on the fact that given just $\sigma$, it is hard to compute either $\sigma_1$ or $\sigma_2$ (as hard as solving Diffle-Hellman problem). In fact, for two combined signatures, the resulting signature is a zero-knowledge proof of knowledge of each individual signature. This can be shown as follows:

Suppose I can control the output of the hash function (i.e., we are using the "random oracle model"), then instead of doing it the correct way as described above, given $(g, h_1, y_1)$, I can compute a fake tuple $(\sigma, h_2, y_2)$ such that the last verification equation above holds. First generate random $a, b$. The compute:

$$y_2=g^a y_1$$ $$h_2=\frac{g^b}{h_1}$$ $$\sigma=\frac{{y_1}^b\cdot g^{ab}}{{h_1}^a}$$

It can be checked that the above values satisfy the aggregate signature verification equation. Yet, I did this without knowing $\sigma_1$. Hence this is zero-knowledge.