Nature of Ed25519
The High-speed high-security signatures paper defining Ed25519 states
Our recommended curve for EdDSA is a twisted Edwards curve birationally equivalent to the curve Curve25519 (…). We use the name Ed25519 for EdDSA with this particular choice of curve.
Thus Ed25519 formally is a signature scheme, not a curve. In the following, we'll try to plot Ed25519's curve. Which is not Curve25519.
Equation for Ed25519's curve
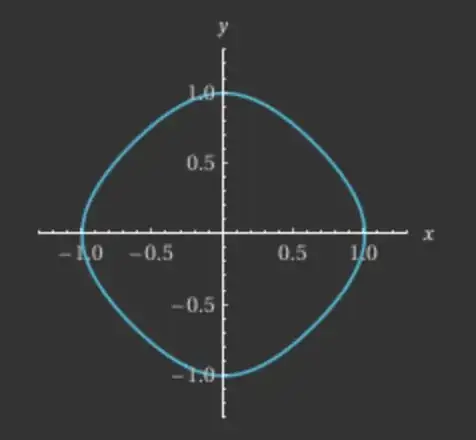
The two figures in the question are for Edwards curves of equation $x^2+y^2=1+d\!\;x^2y^2$, with symmetries w.r.t. lines $x=0$, $y=0$, and $x=y$. Ed25519's curve is a twisted Edwards curve of equation $-x^2+y^2=1+d\!\;x^2y^2$, and the minus sign removes the third symmetry. That's one reason the question's figures do not accurately plot Ed25519's curve.
Plotting $-x^2+y^2=1+d\!\;x^2y^2$ with $d=-300$ in the field $\mathbb R$ as the question does yields
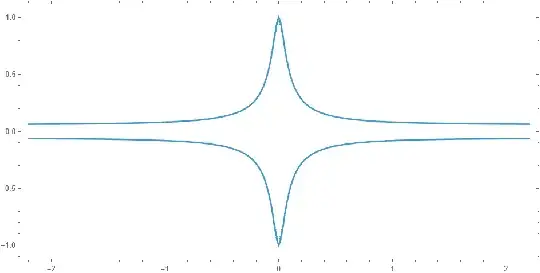
But the above picture uses the wrong field !!
The above is with variables in the field of reals $\mathbb R$, and does not account for parameter $q$ of Ed25519 (the largest 255-bit prime, that is $q=2^{255}-19\,$). It thus does not accurately plot Ed25519's curve, which equation is in the prime field $\mathbb F_q$. That is coordinates $x$, $y$ and parameter $d$ must be in $\mathbb F_q$, with additions and multiplications per the rules for this field.
Crash course on prime fields
A prime field $\mathbb F_q$ is a special case of a ring of integers modulo an integer $n$ (noted $\mathbb Z/n\mathbb Z$ or $\mathbb Z_n$), when that modulus $n$ is a prime $q$. We can view $\mathbb F_q$ as the set of integers in range $(-q/2,q/2)$ [We use that rather than the more common $[0,q)$ in order to keep $0$ at the center, making symmetries more visible]. E.g. for $q=5$ the set is $\{-2,-1,0,1,2\}$, and addition and multiplication tables are:
$$\begin{array}{r|rrrrr}
+&-2&-1&0&1&2\\\hline
-2&1&2&-2&-1&0\\
-1&2&-2&-1&0&1\\
0&-2&-1&0&1&2\\
1&-1&0&1&2&-2\\
2&0&1&2&-2&-1\\
\end{array}
\quad\quad
\begin{array}{r|rrrrr}
\times&-2&-1&0&1&2\\\hline
-2&-1&2&0&-2&1\\
-1&2&1&0&-1&-2\\
0&0&0&0&0&0\\
1&-2&-1&0&1&2\\
2&1&-2&0&2&-1\\
\end{array}$$
Algebra works in the field $\mathbb F_q$ just as in the field of reals $\mathbb R$ when it comes to associativity and commutativity of $+$ and $\times$, their distributivity, $0$ being the neutral for $+$, every element having an opposite, $1$ being the neutral for $\times$, and every non-zero element having a reciprocal. We can define division as multiplication by the reciprocal.
Some notable difference: Fermat's little theorem tells that for all $a\ne0$, it holds $a^{q-1}=1$. This allows computing the reciprocal of $a\ne0$, noted $1/a$ or $a^{-1}$, as $a^{-1}=a^{q-2}$ (there are faster methods, such as the half-extended Euclidean algorithm). And we can test if $x^2=a$ has no, one or two solutions $x$ according to if $a^{(q-1)/2}$ is $-1$, $0$ or $1$, that is according to the sign of the Legendre symbol noted $\left(\frac an\right)$, rather than according to the sign of $a$ as it would be in $\mathbb R$.
What are the points on Ed25519's curve?
Since $x$ and $y$ each can take at most $q$ values, the equation $-x^2+y^2=1+d\!\;x^2y^2$ can be tested for at most $q^2$ candidate points $(x,y)$. With the choices of parameters in Ed25519, it turns out that a little over $1/q$ of these candidates match the equation; and among these, exactly $1/8$ are used by the Ed25519 signature scheme: those that form a prime order subgroup of the elliptic curve group of the points of Ed25519's curve.
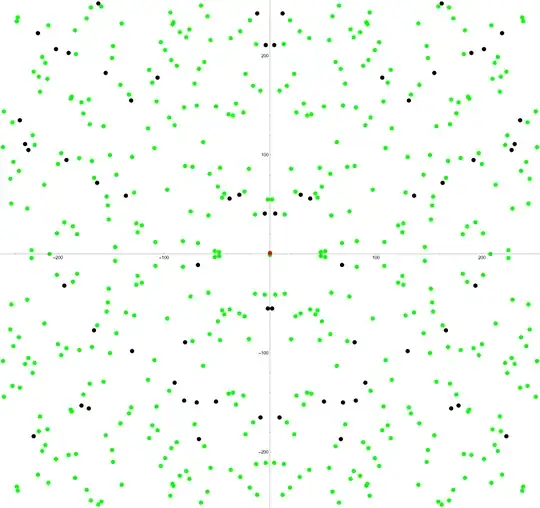
So conceptually, Ed25519's curve consists of points on a square grid of $q\times q$ points, with a little over $1/q$ of the points used, and among these exactly $1/8$ of a special kind. The grid intersections are sparsely populated, and for the naked eye that's randomly, except for symmetries w.r.t. lines $x=0$, $y=0$
Rendering that
There's no way we can represent that down to individually showing each point: with one atom per point, that would be millions times the mass of the milky way. This leaves use with three practical choices:
- Use the actual parameters of Ed25519 and show it's curve from a distance. We'd get a square of uniform color, consisting of mixing the colors of the two kinds of points in a $7/1$ proportion. That would be dull.
- Use the actual parameters of Ed25519 but show only a tiny fraction. On second thought, the points are so sparse that I find computationally challenging to show both all and more than one point in any square we decide to zoom in (except along an axis where we can use symmetries to display two points).
- Use reduced parameters and show the whole curve. We stick to the original design: for some $b\ge10$, $q$ is the largest prime of $b-1$ bit with $q\bmod 4=1$, and $d$ of the form $\frac{1-c}c$ with a small $c$, such that the Legendre symbol $\left(\frac dq\right)=-1$, and the equation $-x^2+y^2=1+d\!\;x^2y^2$ has $8\ell$ solutions with $\ell$ some $b-3$-bit prime. One such choice is $q=2^9-3=509$, $d=-88/89=-184$, $\ell=67$.
With the unity at $(x,y)=(0,1)$ in red, the other $\ell-1=66$ points of the prime order subgroup in black, the other $7\ell=469$ points in green, and points much larger than a grid square so they are visible, we get (click to expand, perhaps re-click to expand more):