Are algorithms like Ascon-PRFshort collision resistant?

Question

I'd like to double check my understanding of the collision resistance of a single unkeyed/public permutation call. I'll use two algorithms as examples, namely Ascon-PRFshort and HChaCha20.

Ascon-PRFshort

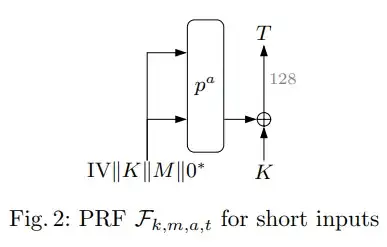
Ascon-PRFshort looks like this and has a 64-bit IV, a 128-bit key, and a message up to 128 bits (any remaining state is set to 0) and outputs a 128-bit tag that's masked with the key (key blinding):

HChaCha20

HChaCha20 has the following state, which goes through the ChaCha rounds like in ChaCha20 but without the feed-forward, and outputs the first and last 128 bits concatenated together to derive a 256-bit subkey:

Questions

1. In these types of examples, if we assume the permutations are ideal/random permutations, is the output collision resistant (even if the key is known/can be controlled)?
2. Can PRFs like these be made collision resistant using Davies-Meyer?

Motivation

I've previously asked cryptographers whilst doing a dissertation about the collision resistance of both algorithms and never received a concrete response. People either didn't reply or didn't know/deferred to proper analysis being needed.

For some reason, collision resistance isn't discussed for these types of KDFs either despite it being a relevant security property. Perhaps the authors think the answer is obvious or no claim is meant to mean it isn't. However, it would be best if authors anticipated potential questions and answered them in the paper/specification, and this doesn't feel like a far fetched question.

Current Thinking

It would seem that ChaCha20 with the feed-forward can be argued to be collision resistant. For some reason, Davies-Meyer is always described in the context of a block cipher from everything I've read, but the term 'feed-forward' is just Davies-Meyer with addition, so it must also be applicable to non-block ciphers.

Without Davies-Meyer, the question seems to be about how much control over the state the attacker has. The standard sponge construction offers limited control due to the rate vs capacity/uninitialised state, whereas these constructions allow most of the state to be controlled. However, they don't allow the entire state to be controlled like the full-state keyed sponge, which is problematic for collision resistance. Therefore, I assume the collision resistance is based on how much state isn't controlled (e.g., the 128-bit constant in HChaCha20).

Answer 1

This is only a partial answer, for which I am not 100% sure. Additionally, the answer below only answers the theoretical/feasibility aspects. Whether any of this applies to a specific primitive is not guaranteed.

Preliminary remark: Due to further clarifications in the comments, my interpretation of the question is about the collision resistance of primitives built from applying a permutation to some inputs and then outputting a truncation of the permutation's output. If the truncation does nothing, the permutation never produces collision. So, the interesting aspect to consider, some truncation of the permutation.

Problem statements:

1. Let $\pi$ be some permutation; in the following, we will consider it as being selected at random. We are interested in constructions of collision resistant PRFs $f: K \times X \to Y$ using an “encode-permute-truncate" kind of construction. In other words, $$y = f(k,x) = \text{TRUNC}(\pi(\text{encode}(k,x))).$$

2. Can one use a generic construction such as Davies-Meyer to add collision resistance to a PRF?

Here, Collision resistance means it is hard for a given adversary to find $(k,x) \neq (k', x')$ and $f(k,x) = f(k',x')$.

Answering question 1: This question has been considered in a few research papers. In particular, in the analysis of the MD6 compression function. Dodis et al. showed that for a given constant $C$, the compression function $h(k,x) = \text{TRUNC}(\pi(C|k|m))$ is indifferentiable from a random oracle. That is to say, it has the properties of a random oracle, including collision resistance.

Application to Ascon-PRF short and HChacha20: My conjecture is that this result would carry over to Ascon-PRFshort and HChacha20, when the underlying permutations are seen as ideal (Though,that's not quite the case with the Chacha permutation). Both seem to integrate a constant in the encoding of the permutation input. In Ascon-PRF, the IV is a constant that summarizes the key and message space. One open question is, what about collisions across different keys and message sizes? My conjecture is that they don't apply since the IV works as a domain separator for different message and key spaces (it's not just a constant for any key and message sizes). In fact, without a careful choice of the IV, Ascon-PRF would not even be a secure PRF.

Answering question 2:

On Davies-Meyer: This construction builds good compression functions with good security. However, their analysis requires the starting point to be a random permutation or an ideal cipher. I don't think building a CR-PRF directly from a PRF using the D-M construction is possible. For a PRF $f$, we can "sabotage" it so for some $(k,x) \neq (k', x')$ we have $f(k',x') \oplus x = f(k',x') \oplus x'$. Nevertheless, $f$ remains a PRF. In other words the "local" behavior doesn't matter much for PRF security.

Interpretation: The above does not mean that Davies-Meyer is always doomed for any PRF. Indeed, if the "PRF" were a blocipher, we have good hope that D-M would produce a collision-resistant function. Instead, the statement above shows that D-M on a PRF should be evaluated on a case-by-case basis, which has limited general applicability.