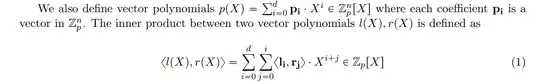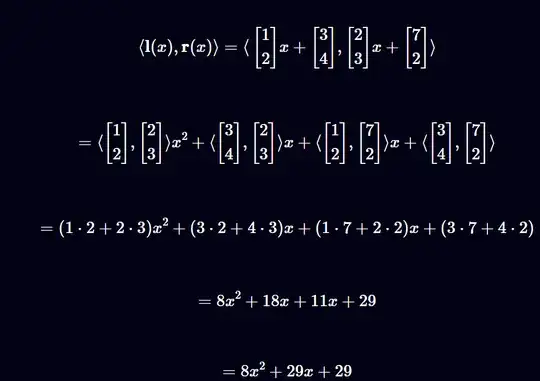Bulletproofs, Vector Polynomials & Inner Product of Vector Polynomials

Question

This is from the Bulletproofs Paper

Page 11

The paper defines what is a vector polynomial & how the inner product of Vector Polynomials are computed.

Now, I am unable to find any text about these anywhere else outside of this paper. Vector Polynomials seem to denote the vector of co-efficients of a polynomial in most other places instead of each co-efficient being a vector like here.

Anyway, my question is about the formula given for calculating inner product of Vector Polynomials

From the paper With $l(X)$ & $r(X)$ as vector polynomials

$<l(X), r(X)> = \sum_{i=0}^d \sum_{j=0}^i <l_i, r_j>\cdot X^{i+j} $

A write up about Bulletproofs is found at the rareskills website

https://www.rareskills.io/post/inner-product-argument

They have computed an inner product of 2 vector polynomials here

The formula they are using seems to be a little different

$<l(X), r(X)> = \sum_{i=0}^d \sum_{j=0}^d <l_i, r_j>\cdot X^{i+j} $

i.e. the paper uses

$\sum_{i=0}^d \sum_{j=0}^i $

while rareskills uses

$\sum_{i=0}^d \sum_{j=0}^d$

i.e. paper iterates $j$ from $0$ to $i$ while rare skills does it from $0$ to $d$

Which is correct - I think rare skills is correct but I am not sure how to confirm it. Also is the concept of Vector Polynomials & their Inner Product defined specifically for this paper or can I find a description outside of the context of bulletproofs?

Answer 1

The upper bound on the $j$ summation in the bulletproofs paper is a typo. This is confirmed by their remark below equation (1) in the paper:

Let $t(X) = \langle \mathbf l(X), \mathbf r(X)\rangle$, then the inner product is defined such that $t(x) = \langle \mathbf l(x), \mathbf r(x)\rangle$ holds for all $x \in \mathbb Z_p$, i.e. evaluating the polynomials at $x$ and then taking the inner product is the same as evaluating the inner product polynomial at $x$.

Taking a simple example, let $$\mathbf l(X)=\begin{bmatrix}1\\ -2\end{bmatrix} + \begin{bmatrix}1\\ 2\end{bmatrix}X$$ $$\mathbf r(X)=\begin{bmatrix}-1\\ 3\end{bmatrix} + \begin{bmatrix}2\\ 2\end{bmatrix}X.$$ Computing $t(X)=\langle\mathbf l(X),\mathbf r(X)\rangle$ using the typoed form in the bulletproofs paper would give $$t(X)=-7+5X+6X^2$$ whereas the corrected version would be $$t(X)=-7+3X+6X^2.$$ Checking these against the quoted remark, let us take $x=1$ so that $\mathbf l(1)=\begin{bmatrix}2\\ 0\end{bmatrix}$, $\mathbf r(1)=\begin{bmatrix}1\\ 5\end{bmatrix}$ and hence $\langle \mathbf l(x), \mathbf r(x)\rangle=2$. On the other hand the bulletproof typoed version yields $y(1)=4$ and the corrected version yield $t(1)=2$ and this latter is consistent with the remark.

Vector polynomials are a natural enough concept and can crop up in multi-dimensional dynamics for example. They given an alternative way to write vectors whose entries are polynomials, as polynomials whose coefficients are constant vectors. For example, suppose I fire a projectile horizontally at 7m/s from the top of a 100m tower. I can described its position as a vector of polynomials: $$\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}7t\\ 100-9.8t^2\end{bmatrix}$$ or equivalently as a vector polynomial: $$\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}0\\ 100\end{bmatrix} + \begin{bmatrix}7\\ 0\end{bmatrix}t+\begin{bmatrix}0\\ -9.8\end{bmatrix}t^2.$$ Notice for example how addition, scalar multiplication and differentiation are all consistent whether applied to the entries of the vector of polynomials or the terms of the vector polynomial. This allows rules of motion such as $\mathbf v(t)=\mathbf u(t)+\mathbf a(t)t$ to be computed in either format and for us to move between formats at will.

TWe'd like it if taking dot products (e.g. for the rule of motion $\langle \mathbf v(t), \mathbf v(t)\rangle=\langle \mathbf u(t), \mathbf u(t)\rangle+2\langle \mathbf a(t), \mathbf s(t)\rangle$) should also have this consistency and it is a simple matter of checking terms to see e.g. that if $$\mathbf l(X)=\begin{bmatrix}l_1(X)\\ l_2(X)\end{bmatrix},\quad \mathbf r(X)=\begin{bmatrix}r_1(X)\\ r_2(X)\end{bmatrix}$$ that the dot product of the vector of polynomials $$l_1(X)r_1(X)+l_2(x)r_2(X)$$ corresponds to the polynomial derived from the corrected formula.

More examples can be found in chapter 5 of Geomtery and its Applications or similar textbooks.