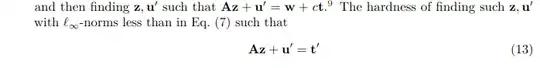 I was reading the Dillithium spec : https://pq-crystals.org/dilithium/data/dilithium-specification-round3-20210208.pdf#equation.6.13
I was reading the Dillithium spec : https://pq-crystals.org/dilithium/data/dilithium-specification-round3-20210208.pdf#equation.6.13
And in the specification, they mention using LWE for key recovery and SIS for forgery. From my understanding, the difference between LWE and SIS is that SIS corresponds to a high-density setting, while LWE can be seen as a low-density SIS instance.
Given this, why does the SIS instance in Equation 13 of Section 6.2.1 look very similar to an LWE instance? Yet in the appendix, it is analyzed as a SIS problem rather than an LWE problem.
Let me know if you'd like me to clarify this further!