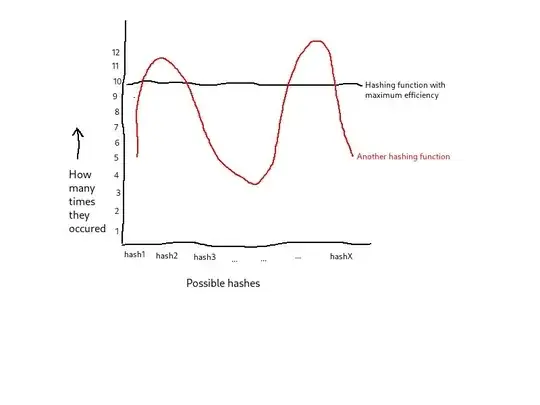
Since all hashing functions have a finite (but quite large) number of hashes. So let's say a hashing function can produce total X hashes. Now I sent it 10X inputs (I know there are computational limits, just for theory). I want to know if all hashes would be repeating roughly 10 times, so basically it would be equally likely to get each hash in the possible set every time? Or some hashes would be much more repetitively visible and some quite less?
Following image to better describe what I mean.
Asked
Active
Viewed 40 times
0
Amit
- 3
- 1
1 Answers
0
It is very unlikely that a good cryptographic function will have the kind of flat empirical distribution that you are asking for, without some structural weaknesses, such as linearity.
Even when we model a hash function by a uniform distribution when we consider (say) throwing $m$ balls into $n$ bins independently and uniformly at random some deviations from a uniform distribution are highly likely.
The answer to the question here goes into a lot of detail about this.
The average "load" of each point will be 10 as soon as $X$ is cryptographicaly large, but with high probability the output with maximum load will have load roughly $$ \frac{m}{n}+\sqrt{\frac{2 m \ln n}{n}}=10 +\sqrt{20 \ln X}, $$ since $m=10X=10n.$
kodlu
- 25,146
- 2
- 30
- 63