I read a paper in which a tree search algorithm (specifically a DPLL SAT solver) is implemented with garbled circuits. In this tree search algorithm, we have (obviously) the typical 'forward' steps and 'backward' steps one would expect to find in a tree search algorithm. Keeping track of the current search position within the tree is done with a stack (also no surprises there; pretty standard solution in my opinion). As the tree search is handling private input, the stack in the implementation is actually an oblivious stack (OS),
How exactly is the OS then integrated in the generated garbled circuits?
My thoughts so far:
From what I understood from this paper is that we can construct a circuit, which does (at most) n search steps. Say we build this circuit as in the picture below, where each block is a step through a search tree (specifically for the mentioned SAT paper, each block is a so-called 'giant step'). In each block we may have to backtrack in the tree, so we need as additional input the oblivious stack for pop and/or push operations.
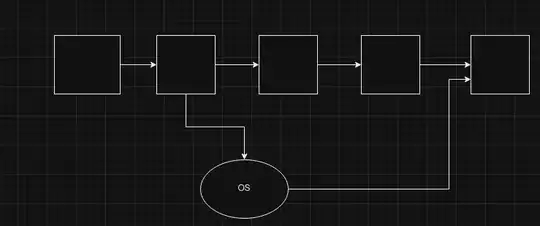
Is my construction of using OS correctly described in the picture? So is the OS simply an external datastructure which holds garbled values as depicted in the image? Independent of the answer to that question, I would like a reference/code sample which helps me understand how this is done on the code level (The source code for the OS of the code repository of the linked SAT solver are unintelligible, also the EMP framework is not documented at all).
Specifically i like to have more context, also answering this question:
- Is an OS itself just the computation of a fancy garbled circuit?