AES-128 if cracked using quantum computer, Grover’s algorithm will make it $2^{64}$ computations to complete.
The fastest non-quantum classical super computer can run approximately $2^{57}$ operations per second, so it would do the $2^{64}$ operations in less than a minute. And I believe the quantum computer would have even faster operation speed. How some people say AES-128 is still quantum-resistant?
To begin with, the threat from Grover (unlike Shor which does not apply to AES) does not lead to a subexponential algorithm, so doubling keylength is sufficient to address it.
More specifically, there are the issues of memory and the huge number of required qubits.
According to this paper by Grassl et al. the required number of quantum gates, depth of quantum circuits, and qubits for AES are as given below. We are currently very far away from such a computer.
Edit: Incorporated a crucial comment from @poncho in the answer for more context
The depth is the real killer. Anything that takes circa $2^{80}$ sequential operations will take, in practice, an infeasible amount of time. Yes, you can try to do things in parallel, but that dilutes the advantage you get from Grover's - for each halving of the time, you end up needing four times as many Quantum Computers. So, to get a T-depth of $2^{60}$ (that is, if each T operation takes a nanosecond, it'll still take over 30 years), you'd need circa $2^{40}$ = a trillion Quantum Computers.
I'll break down a few incorrect assumptions in your question:
AES-128 if cracked using quantum computer, Grover’s algorithm will make it $2^{64}$ computations to complete.
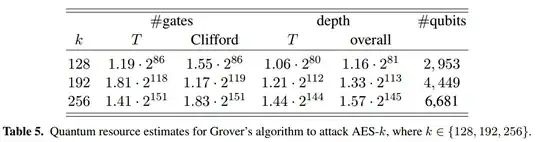
Here "computations" is doing a lot of work. What you mean is: $2^{64}$ coherent evaluations of AES encryption, done in superposition. Each of these evaluations involves quite a few quantum operations: from one of the latest works (https://eprint.iacr.org/2022/683), about 100,000 operations in about 600-700 "cycles" (more on that later)
The fastest non-quantum classical super computer can run approximately $2^{57}$ operations per second, so it would do the $2^{64}$ operations in less than a minute.
This only works because classical super computers are massively parallel: they have enormous numbers of processors working simultaneously. Purely sequential clock speed in supercomputers topped out circa 2013 at around 3-5 Ghz.
As other comments mentioned, Grover parallelizes very badly. If you want it to find the answer twice as fast, you need 4x as many quantum computers. If you want the answer in less than 10 years, you need astronomical amounts of quantum hardware.
And I believe the quantum computer would have even faster operation speed.
I'm not sure why you believe this. Quantum computers won't just be better versions of classical computers. They will be able to do certain specialized tasks with fewer operations, but operations on quantum computers are more complicated. The main issue is noise: it is very hard to protect delicate quantum states.
In fact, with the most plausible approach today to protect against noise, each "cycle" in a quantum computer, as described above, will take many physical rounds of error correction to complete. Last time I did the numbers on this it was about 30 cycles per operation to keep the noise small enough for Grover's search.
So:
When you account for all of this, the cost for a plausible quantum attack is around $2^{136}$ (compared to $2^{143}$ for the classical, measured at roughly the same level at detail). Both attacks are essentially impossible science fiction.
If you've got an hour, I recently gave a talk about this: https://youtu.be/eB4po9Br1YY, where I go through some of the details of the $2^{136}$ number.
