Let us first review the notations. For any $x, u \in \mathbb{F}_2^n$,
$$\pi_u(x) = \prod_{i=1}^n x[i]^{u[i]}$$
where $x[i]^1 = x[i]$ and $x[i]^0 = 1$. Equivalently, we can write
$$\pi_u(x) = \prod_{j\,s.t.\,u[j]=1} x[j]$$
The hamming weight of an element $x$ is denoted by $w_x$, i.e., $w_x = \sum_{i=1}^n x[i]$. Also, the set $S_k^n = \{x \in \mathbb{F}_2^n \,|\, w_x \geq k\}$ is the set of all elements with hamming weight greater than equal to $k$. Now, a multiset $\mathbb{X}$ has $D_{k}^n$ property if
$$\bigoplus_{x \in \mathbb{X}} \pi_u(x) = 0, \forall u \in (\mathbb{F}_2^n \setminus S_k^n)$$
i.e., the parity of $\pi_u(x)$ for all $x \in \mathbb{X}$ is even when $w_u < k$. Let us analyse the division property of the multiset $\mathbb{Y}$ obtained when the element $e_1 \in \mathbb{F}_2^n$ (the binary string with 1 in the first bit and 0 in the remaining) is $\mathsf{XOR}$ed to the multiset $\mathbb{X}$, i.e., $\mathbb{Y} = \{x \oplus e_1 \,|\, \forall x \in \mathbb{X}\}$. Let $u \in \mathbb{F}_2^n$ such that $1 \leq w_u <k$. Consider the case where $u[1] = 1$, then
$$\begin{align*} \bigoplus_{y \in \mathbb{Y}} \pi_u(y) &= \bigoplus_{x \in \mathbb{X}} \pi_u(x \oplus e_1)\\
&= \bigoplus_{x \in \mathbb{X}} \prod_{i=1}^n (x[i] \oplus e_1[i])^{u[i]} \\
&= \bigoplus_{x \in \mathbb{X}} \left( (x[1] \oplus 1)^{u[1]} \prod_{i=2}^n x[i]^{u[i]} \right) \\
&= \bigoplus_{x \in \mathbb{X}} \left( \prod_{i=1}^n x[i]^{u[i]} \oplus \prod_{i=2}^n x[i]^{u[i]} \right) \\
&= \left(\bigoplus_{x \in \mathbb{X}} \prod_{i=1}^n x[i]^{u[i]} \right) \oplus \left( \bigoplus_{x \in \mathbb{X}} \prod_{i=2}^n x[i]^{u[i]} \right) \\
&= \left( \bigoplus_{x \in \mathbb{X}} \pi_u(x) \right) \oplus \left( \bigoplus_{x \in \mathbb{X}} \pi_{\tilde{u}}(x) \right)
\end{align*}$$
where $\tilde{u}[1] = 0$ and $\tilde{u}[i] = u[i], \forall 1 < i \leq n$. In other words, the hamming weight of $\tilde{u}$ is less than the hamming weight of $u$, i.e., $w_{\tilde{u}} < w_{u} < k$. Since $\mathbb{X}$ possesses $D_k^n$ property, both $\bigoplus_{x \in \mathbb{X}} \pi_u(x)$ and $\bigoplus_{x \in \mathbb{X}} \pi_{\tilde{u}}(x)$ are equal to 0.
Now, in the case of $u[1] = 0$, we will have
$$\bigoplus_{y \in \mathbb{Y}} \pi_u(y) = \bigoplus_{x \in \mathbb{X}} \pi_u(x \oplus e_1) = \bigoplus_{x \in \mathbb{X}} \pi_u(x) = 0$$
Repeating this process, we can show that the division property does not change when $\mathbb{X}$ is $\mathsf{XOR}$ed with any constant $a \in \mathbb{F}_2^{n}$ by decomposing $$a = \underset{j\,s.t.\,a[j]=1}{\oplus} e_j$$
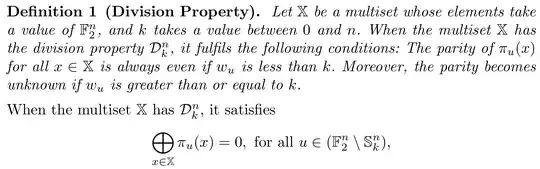Division property is proposed as a generalized integral property at Eurocrypt 2015 by Yosuke Todo in his paper Structural evaluation by generalized integral property, And in paper Integral Cryptanalysis on Full MISTY1.
