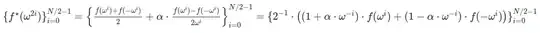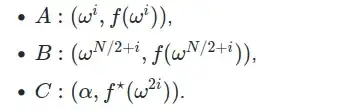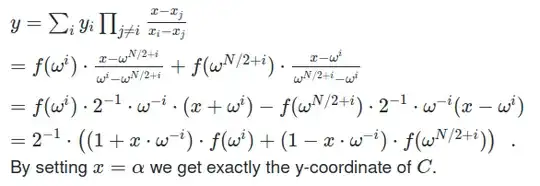Over a few days, I have been trying to understand the FRI protocol discussed in the link https://aszepieniec.github.io/stark-anatomy/fri . It explains Fast Reed-Solomon Interactive Oracle Proof (FRI) protocol using merkle tree polynomial commitment. This protocol is run between a prover and verifier. To enhance my understanding, I tried with this following example.
Example:
Let generator omega (w) = 7, prime p = 17 , N=16.
Field $\mathbb F_p = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 ]$
Let $f(x) = 36 x^5 + 62 x^4 + 19 x^3 + 51 x^2 + 37 x + 97$.
The subgroup $D = [1, 7, 15, 3, 4, 11, 9, 12, 16, 10, 2, 14, 13, 6, 8, 5] = \{w^i\}$ for i = 0 to 15.
Now I computed f(w^i) for i = 0 to 15 using subgroup D list. I got f(w^i) for i = 0 to 15 = [13, 3, 0, 7, 1, 0, 6, 15, 16, 7, 2, 14, 11, 10, 13, 6 ]
Same way I computed f(-w^i) for i = 0 to 15 = [ 16, 7, 2, 14, 11, 10, 13, 6, 13, 3, 0, 7, 1, 0, 6, 15 ].
Now I computed f*(w^2i) i = 0 to 7 using formula depicted in below figure with alpha = 13 and I got [ 12, 11, 16, 1, 11, 13, 12, 9 ].
This is one round of FRI protocol. In all the computations, I used mod 17. I hope I computed all these values correctly. If some value is incorrect, please correct as per the protocol.
Now during verification, I choose value of i = 3 from verifier. I got 3 points A( 3, 7 ) , B( 14, 14 ), C( 13, 12 ).
When I do Lagrange interpolation using formula in below figure, I get L(alpha) = 1 but y-coordinate of C is 12 which shows verification fails.
I am not able to understand where I have gone wrong. Please correct me and give me a case where verification passes successfully. Atleast, please explain a small example where verification becomes successful.
Thank you.