GKR Protocol - is it one Sum-Check per layer or is it one Sum-Check per gate?

Question

I am reading about GKR protocol from Justin Thaler's book - Proofs, Arguments & Zero Knowledge

On Page 59,

In the first message, $P$ tells $V$ the (claimed) output(s) of the circuit. The protocol then works its way in iterations towards the input layer, with one iteration devoted to each layer.

I am a little confused about what exactly iteration means here. Does one iteration means one sum-check proof or can each iteration (corresponding to a layer) contain multiple sum-check proofs?

Page 61, Lemma 4.7

$W_i(z) = \sum_{b,c \in \lbrace 0,1 \rbrace^{k_{i+1}}} add_i (z,b,c)\cdot (W_{i+1}(b)+W_{i+1}(c)) + mult_i(z,b,c)\cdot (W_{i+1}(b)\cdot W_{i+1}(c))$

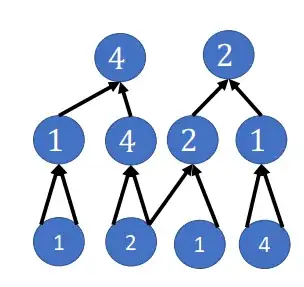
Consider this circuit from Page 65

For e.g. for the circuit above, in the first (topmost) layer, won't we have to run the sum-check protocol for both $W_0(0)=4$ & $W_0(1)=2$ separately? And in the next layer, we will need 4 sum-check protocol runs - $W_1(0,0)=1$, $W_1(0,1)=4$, $W_1(1,0)=2$ & $W_1(1,1)=1$. And so on?

I can think of making it just one sum-check per layer but that will work only if all the gates in that layer are addition gates.

If all the gates in a layer are addition gates, then we can change the sum-check equation to

$\sum_{z \in s} W_i(z) = \sum_{z \in \lbrace 0,1 \rbrace^{log(s)}} \sum_{b,c \in \lbrace 0,1 \rbrace^{k_{i+1}}} add_i (z,b,c)\cdot (W_{i+1}(b)+W_{i+1}(c)) + mult_i(z,b,c)\cdot (W_{i+1}(b)\cdot W_{i+1}(c))$

Where number of gates in that layer is $s$

But this will not work unless all gates in that layer are addition gates.

Answer 1

Short answer

The GKR protocol consists of one execution of the sum-check sum protocol per layer.

Long answer

Considering that a layer has $2^{k}$ gates, the function $W_i: \{0,1\}^k \rightarrow \mathbb{F}$, defined as

$$W_i(z) = \sum_{b,c \in \lbrace 0,1 \rbrace^{k}} add_i (z,b,c)\cdot (W_{i+1}(b)+W_{i+1}(c)) + mult_i(z,b,c)\cdot (W_{i+1}(b)\cdot W_{i+1}(c))$$

maps every gate $z$ of the $i$-th layer to its output value. You should verify and convince yourself about this before continuing the analysis (basically, for each gate $z$, there will be a single pair $(a, b)$, corresponding to the left and right input wires of $z$, thus, only one instance of $add(z, a, b)$ or of $mult(z, a, b)$ will be equal to 1 in the summations in $W$).

Now, what the GKR protocol does is to define a low-degree polynomial extension $\tilde{W}:\mathbb{F}^k \rightarrow \mathbb{F}$ of $W_i$ and it applies the sum-check sum protocol on $\tilde{W}$ running over the variables $a$ and $b$, not on $z$ (so there are not 3 summations as you wrote!).

In other words, for some function $f$, we can write $$\tilde{W}(z) = \sum_{a, b \in \{0, 1\}^k} f(z, a, b)$$ And when given a polynomial $G$ claimed to be equal to $\tilde{W}$, we can pick a random field element $r^\star$ and check if $G(r^\star) = \tilde{W}(r^\star)$. By the Schwartz-Zippel lemma, if this equality is true, then we can assume $G$ and $\tilde{W}$ are indeed equal. However the verifier can only compute $y = G(r^\star)$, but not $\tilde{W}(r^\star)$, since they don't know $\tilde{W}$ (only the prover does).

So, they both run the sum-check protocol (running on all the $2^{k+1}$ possible values for the pairs $(a, b)$) to verify that $$y = \sum_{a, b \in \{0, 1\}^k} f(r^\star, a, b)$$

Notice that if the sum-check sum protocol has a positive answer, we conclude that $y = \sum_{a, b \in \{0, 1\}^k} f(r^\star, a, b)$, thus, $G(r^\star) = \tilde{W}(r^\star)$, thus, $G = \tilde{W}$, thus, all gates of the $i$-th layer were evaluated correctly.

(There is a detail here: at the end of the protocol, the verifier cannot finish the sum-check sum protocol, since this requires evaluating $f(r^\star, a^\star, b^\star)$ for random $r^\star, a^\star, b^\star$. This check is then "shifted" to the next layer and the GKR protocol continues recursively).