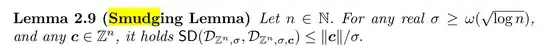A Smudging Lemma in Lattice

Question

I saw a paper LLW21 in EUROCRYPT 2021 that used this lemma, but there was no proof or references.

How should this lemma be proved ？

Answer 1

In general the total variation distance (what you call the statistical distance --- both names are used) between (even continuous!) Gaussians is hard to compute. See for example this. Instead, people often instead compute a different measure of distance between Gaussians, and then use this quantity to bound the total variation distance.

Specifically, in terms of the KL divergence, the bound

$$\Delta(P, Q) \leq \sqrt{\frac{1}{2}\mathsf{KL}(P||Q)}$$

is known as Pinsker's inequality, where $\Delta(P, Q) := \frac{1}{2}\lVert P-Q\rVert_1$ is the Total Variation distance.

Throughout, I will write $P$ for the distribution with pmf proportional to $\exp(-\pi \lVert\vec x\rVert_2^2/\sigma^2)$, and $Q$ for the distribution with pmf proportional to $\exp(-\pi \lVert \vec x-\vec c\rVert_2^2/\sigma^2)$. I'll write the proportionality constants as $C_P$ and $C_Q$.

Anyway, one can compute that

$$\mathsf{KL}(P||Q) = \sum_{\vec x}P(\vec x)\left(\frac{\pi \lVert \vec c\rVert_2^2}{\sigma^2}-2\langle\vec x,\vec c\rangle\right) + \ln(C_P/C_Q)$$

By considering pairs of points $\vec x, -\vec x$ (where $P(\vec x) = P(-\vec x)$), one can see that the $-2\langle\vec x,\vec c\rangle$ term will cancel (it doesn't for the total variation distance, and is the reason why bounding it directly is annoying). For the proportionality constants, it is known (Lemma 2.7) that $C_P \leq C_Q$, under your condition that $\sigma \geq \omega(\sqrt{\log n})$. Applying Pinsker's inequality, and we get

$$ \Delta(P, Q) \leq \sqrt{\frac{\pi}{2}}\frac{\lVert \vec c\rVert_2}{\sigma}. $$

Note that this constant may be an artifact of my normalization of Gaussians. If you use the alternative normalization $\exp(-\lVert \vec x\rVert_2^2/(2\sigma^2))$ that some authors prefer, you get the bound

$$\Delta(P, Q) \leq \frac{1}{2}\frac{\lVert \vec c\rVert_2}{\sigma}$$

I won't check which normalization your paper uses, as either way I imagine the above is good enough for you.

Answer 2

You probably should define $\mathsf{SD}$ and $\mathcal{D}$.

There is a much simpler 1-dimensional version that is proved, see Lemma 2.1 of Asharov-Jain-Wichs, 2011. The proof is one-line:

In [LLW21], $\mathcal{D}$ denotes $n$-dimensional discrete Gaussian. I did not find a proof, but there is another similar lemma with proof (which I did not read): https://eprint.iacr.org/2022/055.pdf