In the Full-State Keyed duplex (sponge construction AEAD), plaintext is absorbed into the entire state of the sponge permutation but only a portion of the output can be used else the scheme breaks (permutation state leaks, key leaks).
How is this data asymmetry in any way useful? You cannot encrypt the block of plaintext you just fed in because of a size mismatch. Yet it is claimed to be more efficient.
In the Full-State Keyed duplex (sponge construction AEAD), plaintext is absorbed into the entire state of the sponge permutation but only a portion of the output can be used else the scheme breaks (permutation state leaks, key leaks).
This is an interesting observation. Indeed, revealing the full state of the sponge would very clearly not be CPA secure. In $\S$7.1 of the cited paper, the authors describe how (ignoring some domain separation & padding bits), in one example construction, the plaintext message is intended to be absorbed in ~$r$-bit (rate) chunks, & the associated data (AD) is simultaneously absorbed into the remaining $c$ (capacity) bits. That is, unless AD is large, in which case Algorithm 3 on page 15 describes how such overflow is handled.
In fact, $\S$3.1 Algorithm 2 on page 4 makes explicit that each $Z_i$ output is exactly drawn from the rate section of the internal state & must not be larger than $r$-bits.
How is this data asymmetry in any way useful? You cannot encrypt the block of plaintext you just fed in because of a size mismatch. Yet it is claimed to be more efficient.
This requires a two-part explanation. The first part is that the full state can be used for absorption of various inputs, reducing the total number of internal permutation calls.
The second part isn't specified by the cited paper directly. It instead describes general wrap / unwrap cipher interfaces. But, it can be assumed from the context of the paper, & the similarities drawn between Full-State Keyed Sponge (FKS) & Full-State Keyed Duplex (FKD), that the various outputs $Z_i$ actually form a stream cipher's keystream bits, which of course, are squeezed out by at most $r$-bits at a time. This stream cipher interpretation means there's no technical issue between any differing sizes of inputs & outputs.
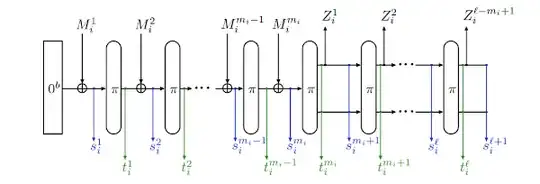
Figure 2 | Full-State Keyed Sponge Algorithm Diagram.
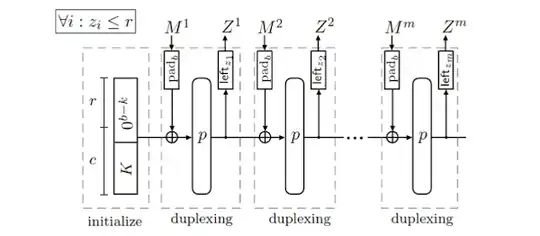
Figure 3 | Full-State Keyed Duplex Algorithm Diagram.
Additionally, $\S$6 Theorem 2 on page 11 shows the adversarial advantage of FKD to be better than or equal to the already provably secure FKS construction(0).
$$ \bf{Adv} \space ^{ind}_{FKD^\pi_0} (B) \le \bf{Adv} \space ^{ind}_{FKS^\pi_0} (B') $$
