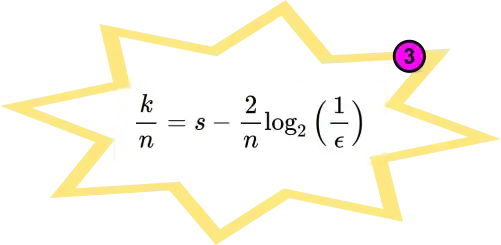5

Assume we want to transform semi-random $n$-bit inputs into shorter $k$-bit outputs computationally indistinguishable from uniformly random bit strings, and there is (in some sense, to be specified) enough entropy in each of the semi-random inputs towards this.

Under what condition(s) on a hash† function (and as far as it's indispensable, on the semi-random input) can we just hash each semi-random input for that randomness extraction purpose? What's a standard name / statement / reference for such condition(s)?

What's the status when the hash is SHA-256 truncated to $k\le256$ bits?

† For some definition of hash including: an efficiently computable function with an $n$-bit input and $k$-bit output, public except perhaps in some limited sense for an auxiliary fixed input. Other conditions are part of the question.

Motivation: that's the question the OP wanted to ask in Can I use a cryptographic hash function such as sha256 for Randomness Extraction?. The body of the question wondered if collision resistance was enough (it's not), and the question got closed by user consensus as duplicate of Can we assume that a hash function with high collision resistance also means a highly uniform distribution?.

fgrieu
  • 149,326
  • 13
  • 324
  • 622

2 Answers2

3

Updates

As discussed in the answer (Caveats) and in the comments, a drawback of what is described below is the independence assumption between the extractor and the seed. This is rather unrealistic in real life since for instance SHA256 may have been used to generate an ephemeral DH scalar via a PRNG and used as well in (un-seeded) HMAC to derive the shared secret. Two papers dealing with these considerations:

I will assume the question is about computational randomness extraction; in particular, we are not in the realm of the impossibility result of extracting randomness with a deterministic function. Additionally, I will assume that the entropy source is independent of the hash function.

With those two assumptions, a sufficient condition (more like assumption) for the hash function is that the hash function "behaves" like a random oracle.

Now, it is well known that a single hash function cannot realize a random oracle. Therefore, the notion of "behave like a random oracle" is not appropriate and cannot be interpreted in the sense of indistinguishable from a random oracle. Instead, we can really on the notion of "Indiffernetiability from a random oracle".

Indifferentiability: The indifferentiability framework introduced by Maurer, Renner and Holenstein describes indifferentiability as a generalization of indistinguishability. Summarized: Let $T$ be a cryptosystem using an idealized but publicly available resource $R$ to realize the ideal cryptosystem $T$. $S$ is said to be indifferentialbe from $T$, if there exists a simulator $\mathcal{S}$ such that "translates" $R$ from the ideal resource $T$. Said differently, for any (efficient) distinguisher $D$, it cannot distinguish between an interaction with $(R, S)$ and with $(\mathcal{S}, T)$. The notion comes with a composition theorem that essentially says that for any cryptosystem $\mathcal{C}$ proven secure when using $T$, and if $S$ and $T$ are indifferentiable., then $\mathcal{C}$ is also secure when using $S$ (There are some caveat).

This is useful in this context since, the framework has been applied to hash functions(Sponges), HMAC.

Hugo Krawczyk also discusses here the role of indifferentiability for the security of HKDF assuming a fixed, zero salt.

Caveats: Now, the arguments above can be contested for a number of reasons: 1) Independence assumptions, 2) Idealizations. Because we assume independence of the source and the underlying hash function (or compression), the answer is not as general as in the case of HKDF with random salts. But the question doesn't state that this assumption is not acceptable. Indifferentiability still requires some idealization (of the underlying compression function or block cipher). However, the value can be seen as a minimization of assumptions: idealizing a compression function seems to be less strong than doing that for a full hash function with structure, etc...

To be as general as possible, I would still use a salted HKDF instead of a single hash function or even HKDF with a zero salt.

Marc Ilunga
  • 4,042
  • 1
  • 13
  • 24
-1

Condition: pass a decent randomness test.

If it looks random downstream, we can be certain that it is truly random if the input driving the extractor function is truly random. You are correct in saying that information theoretic security cannot be achieved just by satisfying output tests without reviewing the entire stack. Thus some understanding of the raw entropy source is necessary, as well as a physical thingie that you can juggle in your hand.

The Left over hash lemma (re-arranged) is:-

rule 3

where we have $n$ = input bits at $s$ bits/bit of raw entropy from the source, $k$ is the number of output bits from the extractor. $\epsilon$ is the bias away from a perfectly uniform $k$ bit length string, i.e. $H(k) = 1 - \epsilon$ bits/bit.

This then allows setting the input/output ratio to choose an output bias $\epsilon$. I use $\epsilon = 2^{-128}$ with SHA-512 because I can. Other ratios for interest are:-

extractors

Having read one or two papers (!) and built many TRNGs that pass all randomness tests, I suggest the term you're looking for is randomness extraction. The quality metric is the Left over hash lemma. Cryptographic functions are not required.

Understand the raw entropy source, pass randomness tests and you're shiny.

Paul Uszak
  • 15,905
  • 2
  • 32
  • 83