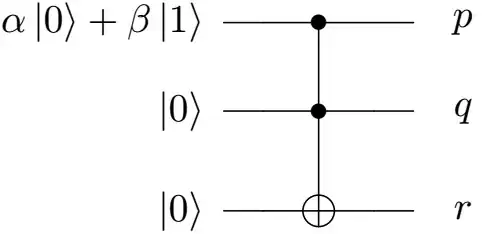
I understand that CNOT and Toffoli (CCNOT) gates are not universal for quantum computation since they (alone) cannot create superposition. Moreover, it is totally possible to perform a CNOT operation where the control qubit is in superposition, $\alpha\vert 0 \rangle + \beta\vert 1 \rangle$, and target qubit to be $\vert 0 \rangle$.
My question is can we have a control qubit to be in superposition while using CCNOT, something like the following?
If yes, what will be the values for $p, q, $ and $r$? If not, why not?
The related material I found are universality of the toffoli gate and CNOT in superposition.
Thank you in advance!