How to enumerate all low-weight undetectable logical errors from a stim circuit?

Question

I have a stim.Circuit instance that is supposed to implement a distance 6 = 7 - 1¹ computation. It turns out that stim.Circuit.shortest_graphlike_error is able to find a undetectable weight-5 error (instead of the expected weight-6)².

But surprisingly (at least to me), simulation results show the theoretical distance-5 circuit has a logical error rate that looks more like a distance ~6.5 code (abusing the definition of distance here) in practice when simulating³.

One explanation I could see to that surprising result is the following: if there are only a handful of low-weight errors and much more higher-weight ones, the low-weight errors may be sufficiently rare to not affect too much the logical error rate.

But to check the validity of that hypothesis, I need a way to list exhaustively all the low-weight errors.

Currently, I am using stim.Circuit.shortest_error_sat_problem and enumerating each error until a weigth-d error is reached. That works, but this method is slow: it takes 1h10m for a distance-5 code with pysat RC2 solver, and I need to simulate at least a distance-7 one because that is where the low-weight errors start to appear.

Is there any more efficient method to check the above hypothesis?

EDIT: I tried to list all the solution containing n <= expected_distance using a regular (non-Max) SAT solver by extracting the hard clauses from the weighted SAT problem output by stim.Circuit.shortest_graphlike_error, but that seems to be way less efficient than the original method.

---

¹: the code should have a distance of 7 at first glance, but due to uncontrollable hook errors that would halve the distance without intervention, I reverse the schedule of stabilizers at each round (see Preserving distance during stabilizer measurements by alternating interaction order from round to round?), theoretically reducing the distance by only 1.

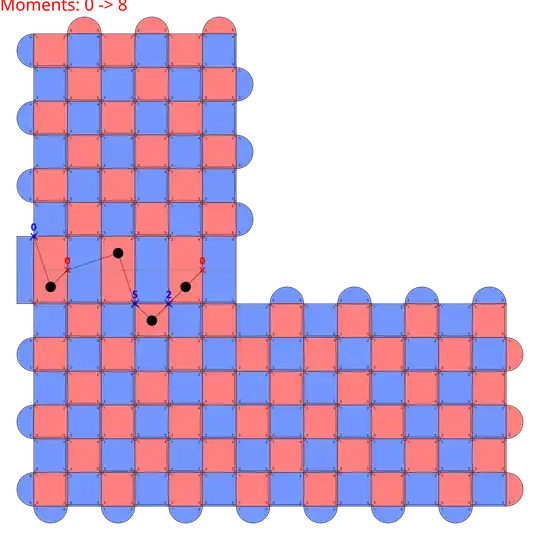
²: The below image show the code and the weight-5 error.

Black dots are detectors triggered by at least one of the errors in the weight-5 error. All the detectors are triggered by an even number of errors, so none of them raise a detection event.

I could not find a way to share the Crumble links (that are quite long) due to a limitation on the number of characters. If you have a good way to reliably share files/links here, please tell me in the comments.

Crumble URL (with detectors annotation, which slow down the UI quite a lot).

Crumble URL (without detectors annotation, should be easier to navigate).

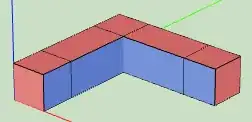
³: To obtain that number, I first took the smallest example possible that has such low-weight errors, which is the following spatial L-shaped bend for an expected distance of 6 = 7 - 1 (i.e., looks like a distance 7 surface code).

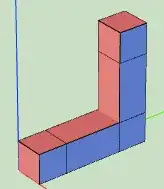
and compared the logical error-rate of its observable to the following temporal L-shaped bend, that does not have the weight-5 errors and implement a regular distance 7 surface code

I expect these two computation to be similar (in fact they perform the exact same computation, the only difference is their practical implementation), and so to have a similar logical error-rate. Simulating these for distance 7 (i.e., a real distance 7 for the temporal bend and a theoretical distance 6 = 7 - 1 for the spatial bend that turns out to be 5 in practice because of the weight-5 undetectable error) shows that they do have a similar logical error-rate under a depolarizing noise:

• at the physical error-rate $10^{-3}$, the spatial bend (effectively distance 5) has a logical error rate that is only ~1.5 times the logical error rate of the temporal bend (effectively distance 7).
• at the physical error-rate $10^{-4}$, the ratio becomes 3.

My "distance 6.5" approximation comes from the above numbers. Because that ratio seems to always be lower than the $\Lambda$ value for any given error rate I tested, the problematic code that is effectively of distance 5 has a logical error rate that looks like a distance $5 < d < 7$ code, closer to 7 than 5.

The original plots and computation up to distance 19 can be accessed here.

Answer 1

What I would do is to use a meet-in-the-middle attack. Enumerate all sets of physical errors with at most 3 errors, and store whether or not the set flips the logical operator in a hash map keyed by the detection event set produced by the error set. Then enumerate all up-to-4 error sets, while checking for each one if its resulting detection event set is in the hash table and maps to the opposite logical flip.

The tools/count_logical_errors script in code.zip from Data for "Magic state cultivation: growing T states as cheap as CNOT gates" does this kind of analysis. In fact I used that tool to justify cutting a round, reducing the fault distance from 5 to 4, because the number of distance 4 errors was negligible so the logical error rate improved despite the distance dropping. That said, the code struggles even on the tiny distance 5 cultivation circuit.

I suspect you'd need to rewrite the attack into C++ to even have a hope at distance 7. Even then, it may take a really long time to run. You may also run into space limitations, and need to make compromises like switching from using a hash table to using a bloom filter. You may need to enforce heuristics like the searched error sets being local.

Really, my recommendation is to just do Monte Carlo sampling to get the logical error rate directly. The distance is just a proxy for that number, so there's no need to obsess over distance when you can directly measure the thing you care about. If the logical error rate is fine, who cares what the distance is.