The semi-classical quantum Fourier transform works by repeatedly preparing a control qubit in a state $R_Z(\phi)|+\rangle$ (where $\phi$ is adapted depending on previous measurements), performing $U^m$ controlled by that qubit to get a phase kickback of $\theta \cdot m$ (where $m$ is a high power of $U$ to scale the kickback, and $\theta$ is the unknown eigenvalue), and then measuring the control qubit in the $X$ basis.
Each step has two inputs (the phase offset $\phi$ and the phase multiplier $m$) and produces one output (the measurement bit). In the usual QFT, each $m$ will be a different power of two and $\phi$ is created by treating the prior measurements as the bits past the decimal point of a binary number.
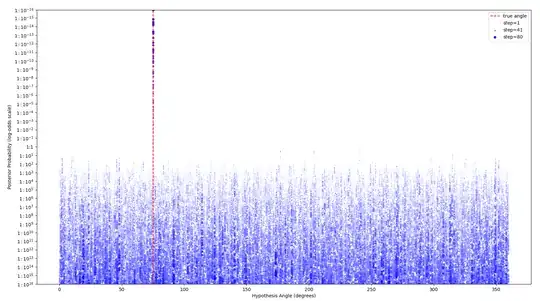
Suppose that instead of picking $\phi$ and $m$ in a structured way, they were simply chosen at random for each step. In the small numerical tests I've done (code at bottom of question) this still converges exponentially quickly towards $\theta$. If you feed the randomly chosen parameters and outputs from each step into a naive Bayesian inference, it quickly picks out the true $\theta$ from the other hypothesis angles:
So great, it works... except naive Bayesian inference requires space proportional to the number of candidate hypotheses. In real algorithms that could easily be $2^{1000}$ different hypothesis angles. The inference needs to be done in a more clever way for a classical control system to actually recover in the angle in practice, if the parameters are being chosen randomly.
Is there a way to do this angle inference problem more efficiently?
Desired Input: a list of phase offsets $\phi_k$, phase multipliers $m_k$, and measurement result bits $b_k$.
Desired Output: the maximum likelihood $\theta$ from $[0, 2\pi)$.
An example application would be making the semi-classical QFT compatible with the Zekendorf representation from https://arxiv.org/abs/2310.00899, where the multipliers are Fibonacci numbers instead of powers of 2.
import fractions
import math
import random
import numpy as np
from matplotlib import pyplot as plt
def probability_of_1_from_phase_kickback(
*,
phase_offset: fractions.Fraction,
eigenvalue_of_state_for_operation: fractions.Fraction,
power_of_operation: int,
) -> float:
"""Probability of the following circuit returning 1 instead of 0:
|0> ---H---Rz(phase_offset)----@---H---M=== result
|
|psi> --------------------------U**m--------- |psi>
Args:
phase_offset: Amount of additional rotation independent of the operation or eigenvalue.
Specified in fractions of a turn (phase_offset=0.5 is a rotation of pi radians).
eigenvalue_of_state_for_operation: The amount of phase kickback expected from applying
the operation U to the test state |psi>.
Specified in fractions of a turn (eigenvalue_of_state_for_operation=0.5 is a rotation
of pi radians).
power_of_operation: How many times U is applied to |psi>, to accumulate phase kickback.
(In practice it's assumed there must be some efficient way to synthesize U**m, rather
than literally applying U a total of m times.)
"""
angle = phase_offset + eigenvalue_of_state_for_operation * power_of_operation
rads = float(angle) * 2 * math.pi
return np.cos(rads / 2)**2
def main():
n = 360*10
hypothesis_angles = [fractions.Fraction(k, n) for k in range(n)]
true_angle = fractions.Fraction(75, 360)
posterior = np.ones(shape=len(hypothesis_angles), dtype=np.float64)
posterior /= sum(posterior)
fig: plt.Figure
ax: plt.Axes
fig, ax = plt.subplots()
ax.vlines(true_angle * 360, 10**-16, 1 - 10**-16, linestyle='--', color='red', label='true angle')
steps = 80
for step in range(steps):
test_multiplier = random.randrange(1, n)
test_angle = fractions.Fraction(random.randrange(1, n), n)
p_actual = probability_of_1_from_phase_kickback(
phase_offset=test_angle,
eigenvalue_of_state_for_operation=true_angle,
power_of_operation=test_multiplier,
)
measurement_result = random.random() < p_actual
for k in range(len(hypothesis_angles)):
p_hypothesis = probability_of_1_from_phase_kickback(
phase_offset=test_angle,
eigenvalue_of_state_for_operation=hypothesis_angles[k],
power_of_operation=test_multiplier,
)
if not measurement_result:
p_hypothesis = 1 - p_hypothesis
posterior[k] *= p_hypothesis
posterior /= sum(posterior)
ax.scatter(
[float(e)*360 for e in hypothesis_angles],
posterior,
label=f'step={step+1}' if step == 0 or step == steps//2 or step == steps -1 else None,
marker='.',
color=(
1 - step / steps,
1 - step / steps,
1),
s=80*(step/steps)**2,
)
ax.set_ylabel("Posterior Probability (log-odds scale)")
ax.set_xlabel("Hypothesis Angle (degrees)")
def probability_to_log_odds(a: float | np.ndarray) -> float | np.ndarray:
mask = (0 < a) * (a < 1)
out = np.empty_like(a)
e = a[mask]
out[mask] = np.log(e / (1 - e))
out[~(0 < a)] = -np.inf
out[~(a < 1)] = np.inf
return out
def log_odds_to_probability(a: float | np.ndarray) -> float | np.ndarray:
mask = (-np.inf < a) * (a < np.inf)
out = np.empty_like(a)
e = np.exp(a[mask])
out[mask] = e / (1 + e)
out[~(-np.inf < a)] = 0
out[~(a < np.inf)] = 1
return out
ax.set_yscale("function", functions=[
probability_to_log_odds,
log_odds_to_probability,
])
m = 16
ax.set_ylim(10 ** -m / (10 ** -m + 1), 10 ** m / (10 ** m + 1))
ax.set_yticks([10 ** k / (10 ** k + 1) for k in range(-m, m+1)], labels=['1:1' if k == 0 else f'<span class="math-container">$1 : 10^{{{-k}}}$</span>' for k in range(-m, m+1)])
ax.legend()
plt.show()
if name == 'main':
main()