How to measure the irregular stabilizers, as in "A Game of Surface Codes"?

Question

I have been going through A Game of Surface Codes: Large-Scale Quantum Computing with Lattice Surgery; however, I am running into issues understanding the "irregular" stabilizers, first shown in figures 39 and 40.

Specifically, I am confused by the blue, rectangular stabilizer; rectangular dark/light stabilizer; and the square, bi-color stabilizer. I am wondering, what is the circuit structure for measuring these stabilizers.

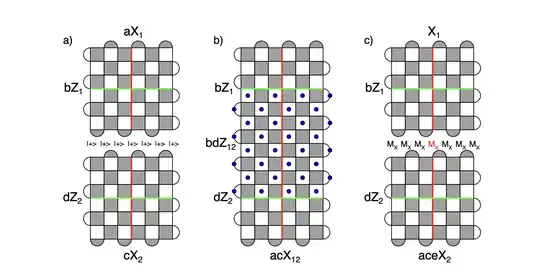
Figure 39 shows the ancillary/data qubit arrangements; however, I am unsure how to deduce the circuit structure/schedule from that. Is there a good resource with this information?

I believe that figure 14 in Lattice Surgery with a Twist: Simplifying Clifford Gates of Surface Codes shows how the bi-color, square stabilizers are measured; but, please correct me if that is incorrect.

I am especially interested in how to measure these stabilizer in a way that only uses nearest-neighbor operations. Do you utilize swap gates?

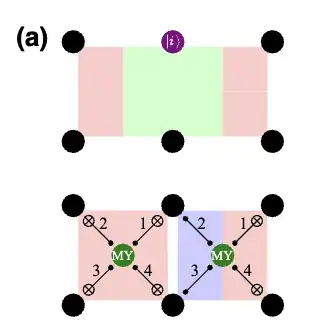
Finally, when you have two boundary stabilizers that share an ancillary qubit -- as you do in the second step of the Y basis measurement depicted in the following figure -- how do you account for this in the scheduling of the stabilizer measurements? Do you just measure one stabilizer, reset the ancillary, and then measure the other stabilizer? Won't this make the stabilizer measurements for the neighboring patches longer? Is there a better way, or simply a necessary step?

Answer 1

I am especially interested in how to measure these stabilizer in a way that only uses nearest-neighbor operations. Do you utilize swap gates?

You can measure these kind of stabilizers using nearest-neighbor operations using "tangling schedules" as described in Tangling schedules eases hardware connectivity requirements for quantum error correction. Using swap gates will probably lead to a reduction of the distance.

For example, here is the circuit shown in figure 9 of the paper that measures XXYXX (the middle qubit in the top row is not part of the measured stabilizer).

Finally, when you have two boundary stabilizers that share an ancillary qubit -- as you do in the second step of the Y basis measurement depicted in the following figure -- how do you account for this in the scheduling of the stabilizer measurements? Do you just measure one stabilizer, reset the ancillary, and then measure the other stabilizer? Won't this make the stabilizer measurements for the neighboring patches longer? Is there a better way, or simply a necessary step?

I think the only way around this is such that the weight two stabilizers aren't in the same columns (as shown in the picture below taken from Low overhead quantum computation using lattice surgery) If this is not possible you can add an extra row/column of qubits inbetween the two patches.