How to initialize the Surface Code in the $\pm Y_L$ State, perform logical $Y$-basis measurement, and $S$ logical gate clarification?

Question

I am trying to learn more about logical state initialization, logical operators, and measurement for the surface code. I am having some trouble understanding the nitty-gritty details of the logical $\pm Y_L$ initialization and logical $Y$ measurement.

I started my investigation from here : How are logical operators performed and measured on the surface code, in a defect-free way?

Which I found to be pretty clear with respect to the $\pm Z_L$ and $\pm X_L$ initialization and measurements.

For the $Y$ logical initialization and measurement, the answer refers to the paper Inplace Access to the Surface Code Y Basis, which I found to be somewhat confusing. I believe this is due to my lack of understanding with regards to the "defect diagrams" in the paper.

I was able to find this helpful slide-deck on Understanding Defect Diagrams, from this post What is the point of defect diagrams?.

Now, for the $Y_L$ basis initialization and measurement, I am looking at the "Y Basis Memory Experiment" portion of this figure from the aforementioned paper:

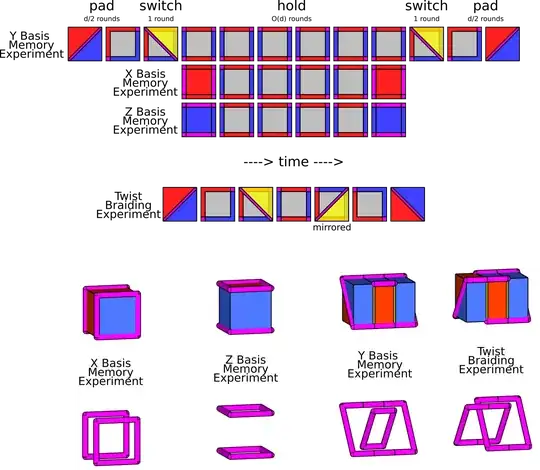
I think that the first three "slices" of the $Y$ memory circuit are the $Y_L$ initialization; however, I would like some clarification on how these slices are implemented and how you obtain $+Y_L$ or $-Y_L$ specifically.

• In the first slice, my understanding is that the data qubits in the red region will be reset to $+X$ and the data qubits in the blue region will be reset to $+Z$; now, are the qubits along the pink diagonal reset to $+Y$? do you reset them to $+Y$ if you want to initialize $+Y_L$ and reset them to $-Y$ if you want to initialize $-Y_L$? If you do not reset the data qubits along the diagonal to $\pm Y$, what do you set them to?
• Now, for the second slice, my understanding is that you will "turn on"/measure the stabilizers depicted in the bottom-right figure of this diagram for $d/2$ rounds, using the standard surface code stabilizer measurement circuit and schedule.
• For the third slice, labeled switch, I understand that this step is related to the circuit steps shown in the preceding figure; however, it is not clear to me how you go in reverse, if that is even the right way of thinking about it.

The $Y$ basis measurement would then seem to be composed of the last three slices of the $Y$ Memory sequence.

• The step labeled switch, would seem to be the circuit steps shown in the preceding figure, directly as shown.
• The next step would then seem to be $d/2$ rounds of standard surface code stabilizer measurement for the stabilizers shown in the bottom-right figure of the preceding diagram. Essentially the same as the second step in the initialization.
• Finally, it would seem you measure the data qubits in the red region in the $X$ basis, and data qubits in the blue region in the $Z$ basis. So, then, do you measure the data qubits along the diagonal in the $Y$ basis? Is the logical $Y$ measurement outcome then the product of these single qubit $Y$ basis measurements along the diagonal?

Logical Phase (S) gate clarification:

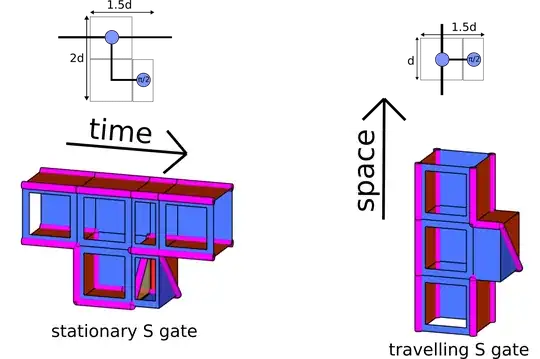
Firstly, I am unclear on how the second "traveling S gate" would work in practice; I just don't understand the defect diagram.

Secondly, for the stationary S gate, I would like some clarification on the steps:

• First, you extend the logical patch down, so you have a d x 2d patch, perform d rounds of standard surface code stabilizer measurements.
• Next, it seems that the two patches are split, followed by a $Y$ basis measurement on the lower patch.
• Question, is there any conditional operation on the un-measured logical patch, depending on the $Y$ basis measurement outcome?

Thank you for taking the time to look over this and I appreciate all of your time and assistance.

Answer 1

now, are the qubits along the pink diagonal reset to +Y?

This is a common misinterpretation of the diagram. The pink lin is just highlighting that X basis resets are transitioning into Z basis resets. All the resets are X (on one side) and Z (on the other side). Think of the pink line as passing between the resets.

Remember, in these diagrams pink lines mean "X error chains can turn into Z error chains using only errors near here". This is vacuously true where X basis resets are next to Z basis resets, because a Z error chain can terminate on the Z basis reset while an X error chain appears out of the X basis reset (thus "turning Z into X"). That's why the pink line appears wherever X basis resets border Z basis resets. It's very similar to the reason pink pipes follow the corners of surface code patches in the spacetime diagrams: that's where X and Z boundaries meet. X excitations can "turn into" Z excitations at these meeting points via the X excitation going into the X boundary while a Z excitation emerges from the Z boundary.

do you reset them to +Y if you want to initialize +YL and reset them to −Y if you want to initialize −YL

Those states differ by Pauli gates, so their initialization is identical as far as the quantum operations are concerned. You just have the classical control system track, propagate, and account for the logical Pauli that flips one into the other. Only Clifford differences require different instructions to be sent to the quantum computer.

do you measure the data qubits along the diagonal in the Y basis?

No, it's the same as with the resets. The pink line just indicates where the data measurement basis changes from X to Z.

The paper's zenodo upload includes stim circuits with all the physical operations, and code for generating these circuits, so you can check exactly the operations being performed instead of guessing. The Y basis init also happens to be one of crumble's example circuits.

Is the logical Y measurement outcome then the product of these single qubit Y basis measurements along the diagonal?

No, it's the product of the set of measurements it disappears into at the end of figure 8 (the circled ones):

The later rounds are only there to error correct these measurements. You can find topologically equivalent observables that terminate later in the circuit, so that they depend on data measurements at the end, but it's likely they also depend on some of the measurements from this round so it's simpler to write code that just terminates it here.

is there any conditional operation on the un-measured logical patch, depending on the Y basis measurement outcome?

There's a conditional Pauli Z, but as mentioned before this doesn't change the instructions sent to the quantum computer. So it never appears in defect diagrams or in ZX calculus graphs (which implicitly postselect into the no-feedback case). Pauli corrections of this kind (using feedback to force a lattice surgery construct to implement a stabilizer ZX graph) can be determined automatically, but yeah it's annoying to figure out what's going on when you're not used to it.