2

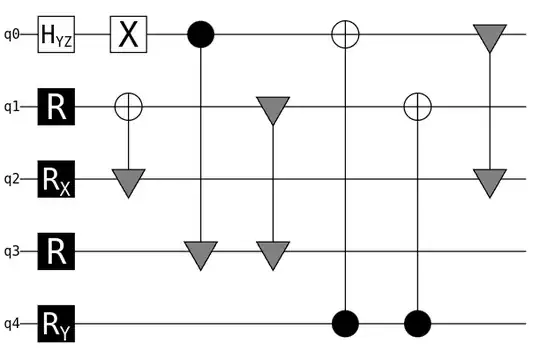
In Chapter 4 of Daniel Gottesman's thesis, he gave an encoding circuit for the famous $[[5, 1, 3]]$ code. 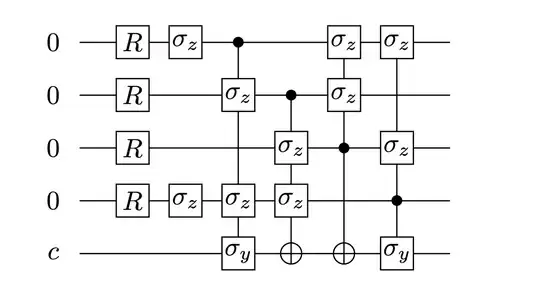enter image description here

Note that in this figure, $R$ is the Hadamard gate. However, this circuit seems not working properly to me. An encoding circuit should propagate physical $Z$ operators to stabilizer generators. In this circuit, the physical $Z$ on the first qubit will be propagated to $XIZIY$, which is apparently not correct as all stabilizer element of the $[[5, 1, 3]]$ should be weight-4. I also checked other $Z$ operators and they all don't give the right stabilizer generators.

The encoding circuit is obtained by his algorithm from the standard form of stabilizer codes. I also applied his algorithm to the standard matrix of $[[5, 1, 3]]$ code, and I got the same circuit. Therefore, I believe there should't be any typos in the figure, and the algorithm itself may be incorrect.

I also have access to the correct encoding circuit like in Fig 3(a) here[arXiv]. I wanna decipher the potential missing part of Daniel's algorithm, but failed. So I am wondering, what is the full algorithm to get encoding circuit from standard form? At least, I would like to know what is the mistake presented in this $[[5, 1, 3]]$ encoding circuit.

FDGod
  • 3,000
  • 2
  • 7
  • 31
Yunzhe
  • 1,449
  • 4
  • 20

2 Answers2

3

I can confirm the circuit is incorrect.

import stim
circuit = stim.Circuit("""
    RX 0 1 2 3
    Z 0 3
    CZ 0 1 0 3
    CY 0 4
    CZ 1 2 1 3
    CX 1 4
    CZ 2 0 2 1
    CX 2 4
    CZ 3 0 3 2
    CY 3 4
""")
for desired_flow in [
    stim.Flow("1 -> XZZX_"),
    stim.Flow("1 -> _XZZX"),
    stim.Flow("1 -> X_XZZ"),
    stim.Flow("1 -> ZX_XZ"),
    stim.Flow("1 -> ZZX_X"),
    stim.Flow("X4 -> XXXXX"),
    stim.Flow("Z4 -> ZZZZZ"),
]:
    if not circuit.has_flow(desired_flow):
        print(f"missing flow: {desired_flow}")
    else:
        print(f"has flow: {desired_flow}")

has flow: 1 -> XZZX_
missing flow: 1 -> _XZZX
missing flow: 1 -> X_XZZ
missing flow: 1 -> ZX_XZ
missing flow: 1 -> ZZX_X
missing flow: ____X -> XXXXX
has flow: ____Z -> ZZZZZ

I also have access to the correct encoding circuit

You linked to an out-of-place encoding circuit that uses 12 two-qubit gates and an extra workspace qubit. That's quite inefficient. There's an inplace encoding circuit with 6 two-qubit gates:

import stim
circuit = stim.Circuit("""
    R 3 1
    RY 4
    RX 2
    H_YZ 0
    X 0
    XCY 1 2
    YCZ 3 0
    YCY 3 1
    ZCX 4 0
    ZCX 4 1
    YCY 0 2
""")
assert circuit.has_all_flows([
    stim.Flow("1 -> XZZX_"),
    stim.Flow("1 -> _XZZX"),
    stim.Flow("1 -> X_XZZ"),
    stim.Flow("1 -> ZX_XZ"),
    stim.Flow("1 -> ZZX_X"),
    stim.Flow("X0 -> XXXXX"),
    stim.Flow("Z0 -> ZZZZZ"),
])

circuit.diagram('timeline-svg')

enter image description here

circuit.decomposed().diagram('timeline-svg')

enter image description here

Craig Gidney
  • 47,099
  • 1
  • 44
  • 119
3

In the errata of Gottesman's thesis (link) he explains how to modify his algorithm and circuits. This paper (link) has a correct algorithm with pseudocode.

Pei-Kai Tsai
  • 76
  • 4