At the moment I am trying to implement variational imaginary time evolution in Pennylane from scratch. To get a feeling if it works, I compare the results of my own implementation with the solutions of the VarQITE class of Qiskit.
I implemented all necessary cicuits for a MaxCut problem and suitable Ansatz. When I also implement the necessary things in Qiskit and compare the two, I find that they do not quite match. My implementation takes longer to converge to the optimal solution and sometimes there are spikes in the energy path. To understand what the Qiskit version does differently, I am trying to understand their code, which I am having trouble with.
Like I undestand from https://quantum-journal.org/papers/q-2019-10-07-191/pdf/ and other sources, to simulate imaginary time evolution one uses the McLachlan’s variational principle and we get the evolution of the parameters by the differential equation.
$$ \sum_{j} A_{ij} \dot{\theta_j} = C_i $$
From this we can get the time derivative of the parameters by calculating the A-matrix and C-vector. The elements of these can be measured by quantum circuits, like this one for the elements of the A matrix:
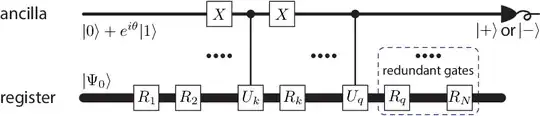
How to use the VarQITE class I got from https://qiskit-community.github.io/qiskit-algorithms/tutorials/11_VarQTE.html and the code that I use is:
from qiskit_algorithms import VarQITE
from qiskit.primitives import Estimator
from qiskit_algorithms.time_evolvers.variational import ImaginaryMcLachlanPrinciple
var_principle = ImaginaryMcLachlanPrinciple()
aux_ops = [Hamiltonian]
evolution_problem = TimeEvolutionProblem(Hamiltonian, time, aux_operators=aux_ops)
var_qite = VarQITE(Ansatz, init_params, var_principle, Estimator())
evol_result = var_qite.evolve(evolution_problem)
To understand how their code works, I looked at the VarQITE class and tried to understand how the evolve( ) function works. But I dont find the circuits for determining the A-matrix and C-vector elements anywhere. Are they doing it differently? If yes does anyone understand how Qiskit is doing it.
Thanks in advance for any input.