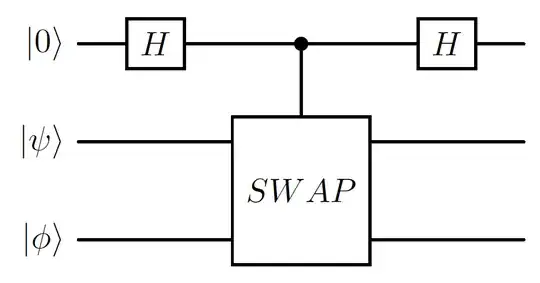
On p. 7 of this paper (https://arxiv.org/abs/2112.04958) it is claimed that: "For any two states $|φ\rangle$ and $|ψ\rangle$ with the same dimensions, the fidelity $F(|φ\rangle, |ψ\rangle)$ can be measured as the output of an ancillary qubit $|a_{anc}\rangle$ after the following operation:
$H_{anc} ⊗ I (cSWAP) H_{anc} ⊗ I |0_{anc}\rangle ⊗ |φ\rangle ⊗ |ψ\rangle$"
Where the fidelity is related to the inner product by $F(|φ\rangle, |ψ\rangle) = |\langle φ|ψ\rangle|^2$, $H_{anc}$ is the Hadamard gate acting on the ancillary state $|0_{anc}\rangle$ and $cSWAP$ swaps the $|φ\rangle$ and $|ψ\rangle$ qubits and is controlled by the ancillary state $|0_{anc}\rangle$.
How can it be proved that this expression of three operators computes the fidelity of $|φ\rangle$ and $|ψ\rangle$? I am trying to represent the operation in terms of $8$x$8$ matrices but I am confused by the placement of the convolution operations: it seems as if $H_{anc}$ acts on $|0_{anc}\rangle$, $I (cSWAP) H_{anc}$ acts on $|φ\rangle$, and $I$ acts on $|ψ\rangle$. But this could not possibly be the case as $|φ\rangle$ and $|ψ\rangle$ should be swapped? Am I misinterpreting how the convoluted operators act on the composite space state?