2

It is clear that a Clifford feedback is necessary for performing a non-Clifford gate with measurement-based quantum computing (for example with Lattice surgery in surface codes).

But, given many logical qubits and non-Clifford gates, can you delay any feedback to the very end of the circuit without modifying anything along the way?

Mathematically, can you always find a Clifford operator $C_2$ such that $C_2P=PC_1$ for any Pauli projection operator $P$ and Clifford operator $C_1$?

If so, is it true to say that you do not need any real-time feedback (or gate modification) apart of just before the final measurement of the computational qubits?

Yaniv Kurman
  • 77
  • 2

2 Answers2

2

That's right, a surface code computation that only performs Clifford gates can be performed without any feedback. Tracking the errors is sufficient to correct them. The corrections can be done entirely in the classical post-processing, without sending any new microwave pulses to the quantum chip.

With non-Clifford gates, there is some necessary feedback. For example, whenever you perform a T in the surface code it may instead be a T dagger, requiring an S gate correction. There's no hard deadline on doing that S correction, and if you're using delayed choice corrections then it doesn't even really impede continuing the computation. But if you accumulate corrections faster than you resolve them, then you will quickly run out of storage space. Consequently, the rate at which you can resolve chains of corrections (the "reaction time" of the system) becomes a limiting factor on the speed of the computation.

Craig Gidney
  • 47,099
  • 1
  • 44
  • 119
1

I'm not sure I understand why your "mathematically" statement implies that you can delay feedback to the end of the circuit. However, there is a construction that allows you to delay feedback until the end of the circuit, but requires you to hold an additional ancilla qubit for every $T$ gate in your circuit. Provided your circuit is only polynomially long, this only requires a polynomial space overhead, but it could be significant.

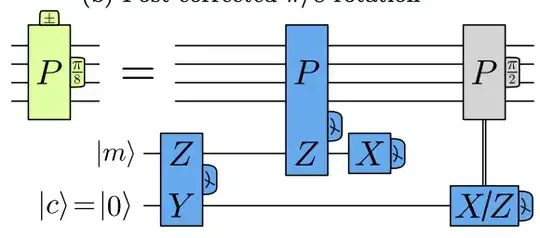
Post-corrected pi/8 rotation

This is from Fig. 25 of Litinski's Game of Surface Codes paper. It allows you to choose whether a teleported $\pi/8$ rotation (generalized T-gate) is replaced by its hermitian conjugate ($-\pi/8$ rotation) by measuring an ancilla "control" qubit in either the X or Z basis. It also does not require any Clifford correction, but only a Pauli correction.

This means you can execute your entire circuit without any Clifford corrections. The Pauli corrections will change some $T$ gates to $T^\dagger$ gates when you commute the Pauli corrections to the end of the circuit, but you can decide whether you implement a $T$ or $T^\dagger$ by changing the measurement basis of that gate's control qubit. The lack of Clifford corrections plus the ability to replace a $T$ gate with $T^\dagger$ after the teleportation allows you to delay feedback until the end.

Note, however, that you'll have to perform your end-of-the-line measurements sequentially, not in parallel. Measuring the control qubit of the first $T$ gate tells you what Pauli correction occurred, which tells you if the subsequent $T$ gates should be replaced with $T^\dagger$s. So before you measure the control qubit of the $n$th $T$-gate, you need to have measured all the control qubits of the $T$ gates before that $T$ gate that could introduce Pauli corrections that affect the $n$th $T$ gate, so you know if it should be replaced by $T^\dagger$.

Jahan Claes
  • 1,312
  • 6
  • 15