Applying Trotterization to a Hamiltonian for Time Evolution in Qiskit

Question

I'm currently working on a project where I need to simulate the time evolution of a quantum system using Qiskit. The Hamiltonian of my system is given by:

$$H = -J \sum_{j=1}^{N-1} (\sigma_j^x \sigma_{j+1}^x + \sigma_j^y \sigma_{j+1}^y) + U \sum_{j=1}^{N-1} \sigma_j^z \sigma_{j+1}^z + \sum_{j=1}^{N} h_j \sigma_j^z $$

I want to use the Trotter-Suzuki decomposition to approximate the time evolution operator, which is given by: $$e^{iH\Delta t} = \prod_j A^j \prod_{j \, \text{even}} B^j \prod_{j \, \text{odd}} B^j + O((\Delta t)^2)$$ where $$A^j = e^{-ih_j\sigma^z_j \Delta t}$$ and $$B^j = e^{-i(U\sigma^z_j\sigma^z_{j+1} - J(\sigma^x_j\sigma^x_{j+1} + \sigma^y_j\sigma^y_{j+1}))\Delta t}$$

In a paper that I'm working on they shown this scheme as the following:

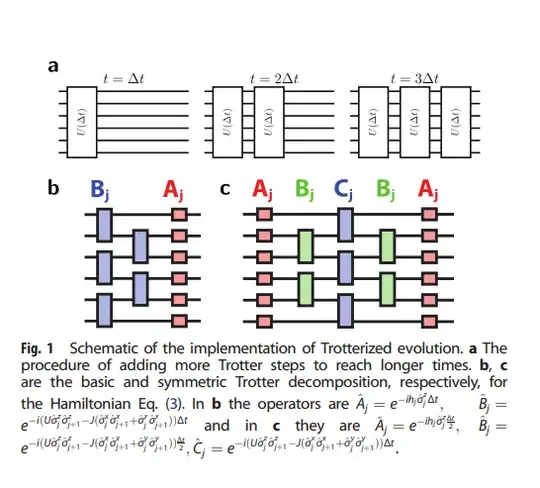
I've tried to solve this by using the following code

The part where I've created my Hamiltonian and its corresponding circuit:

def construct_TFIM_circuit(N_qubit=6,initial_spin_config="domain_wall",
                           Type="XX_chain",J=1,t=1):
    qc = QuantumCircuit(N_qubit)
    if Type=="XX_chain":
        h=np.random.rand(N_qubit)*0  
        U=0
if initial_spin_config=="neel":
    for j in range(N_qubit):
        if j % 2 == 0:
            qc.x(j) 
elif initial_spin_config=="domain_wall":
    for j in range(N_qubit):
        if j < (N_qubit/2):
            qc.x(j) 



state_vector=[]
loc_magnetization=[]
Infos={}

for j in range(N_qubit):
    # Build the evolution gate
    H=  (U * Z^Z ) - (J*X^X)-(J*Y^Y) 
    evo_H= PauliEvolutionGate(H, time=t)
    if j!=N_qubit-1:
        qc.append(evo_H, [j,j+1])
for j in range(N_qubit):        
    qc.append(PauliEvolutionGate(h[j]*Z, time=t), [j])    

It seems like it crates the desired circuit since it matches with the given figure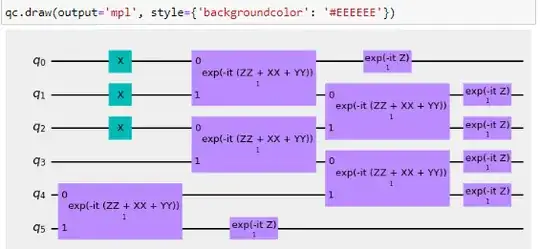

Then I tried to get local magnetization expectations with the variable loc_magnetization for jth spin by the formula $$M_j(t) = \langle \psi(t) | \sigma^z_j | \psi(t) \rangle $$ with the code part(in the same function):

state_vector=Statevector.from_instruction(qc)
Exact=[]
Sampled=[]
for j in range(N_qubit):
    Op_circ=QuantumCircuit(N_qubit) 
    Op_circ.z(j)
    op=CircuitOp(Op_circ)
psi = CircuitStateFn(qc)
psi._statevector = state_vector   # Set the statevector manually



# Exact & Sampled expectations
(M_j_exact,M_j_sampled)=find_expectation(op,psi)
# loc_magnetization have (Exact,Sampled) pair values
loc_magnetization.append((M_j_exact,M_j_sampled))



Infos["JT"]=J*t
Infos["State"]=state_vector
Infos["loc_magnetization"]=loc_magnetization

return (qc,Infos)

However my result doesn't match with the desired expectation, can anybody tell where I'm doing wrong?