In the swap test, how is the final probability $P(0)$ calculated?

Question

Does anyone know much about quantum dot product:

Lets say:

$$|\psi \rangle = \frac{|0\rangle_1|\overrightarrow{x_i}\rangle_2 + |1\rangle_1|\overrightarrow{x_j}\rangle_2}{\sqrt 2}$$ $$|\phi \rangle = \frac{\|\overrightarrow{x_i}\| |0\rangle_1 - \|\overrightarrow{x_j}\| |1\rangle_1}{\sqrt Z}.$$

and assume Z is given $$ Z = \|\overrightarrow{x_i}\|^2 + \|\overrightarrow{x_j}\|^2 $$

Now feeding $| 0 \rangle_1|\psi \rangle_2|\phi \rangle_3$ into the following dot product gate and take a projective measurement in "0" $| 0 \rangle$ in the basis of {$| 0 \rangle$, $| 1 \rangle$}

Which is essentially $\frac {1}{2}(| 0 \rangle_1|\psi \rangle_2|\phi \rangle_3 + | 1 \rangle_1|\psi \rangle_2|\phi \rangle_3 + | 0 \rangle_1|\phi \rangle_2|\psi \rangle_3 - | 1 \rangle_1|\phi \rangle_2|\psi \rangle_3)$ (1) before measurement.

Now I was told that the Probability of "0" is $P(0) = \frac{1}{2}(1+\frac{\|\overrightarrow{x_i} - \overrightarrow{x_j}\|^2}{2Z})$ (2)

But I cannot derive the steps between (1) and (2), can someone perhaps show me the way?

---

Cross-posted on physics.SE

Answer 1

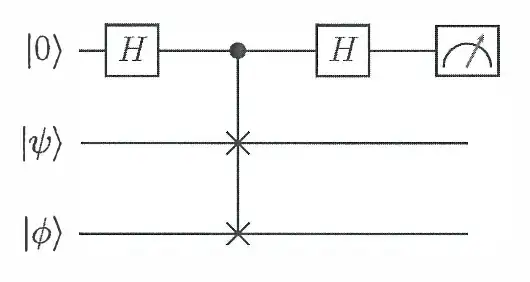
Note that

\begin{align}|\psi \rangle &= \frac {1}{2}(| 0 \rangle_1|\psi \rangle_2|\phi \rangle_3 + | 1 \rangle_1|\psi \rangle_2|\phi \rangle_3 + | 0 \rangle_1|\phi \rangle_2|\psi \rangle_3 - | 1 \rangle_1|\phi \rangle_2|\psi \rangle_3) \\ &= \dfrac{1}{2} |0\rangle \bigg( |\psi\rangle_2 |\phi \rangle_3 + |\phi\rangle_2 |\psi\rangle_3 \bigg) + \dfrac{1}{2}|1\rangle \bigg( |\psi\rangle_2 |\phi\rangle_3 - |\phi\rangle_2|\psi\rangle_3 \bigg)\\ &= \dfrac{1}{2} |0\rangle \bigg( |\psi\rangle |\phi \rangle + |\phi\rangle |\psi\rangle \bigg) + \dfrac{1}{2}|1\rangle \bigg( |\psi\rangle |\phi\rangle - |\phi\rangle|\psi\rangle \bigg)\\ \end{align} I just removed the subscript in the last equation as it's not really needed.

Then we have that

\begin{align} P(0) &= P(|0\rangle) = \big| \langle 0| \psi \rangle \big|^2 \\ &=\bigg| \dfrac{1}{2} \langle 0 |0\rangle \bigg( |\psi\rangle |\phi \rangle + |\phi\rangle |\psi\rangle \bigg) + \dfrac{1}{2} \langle 0|1\rangle \bigg( |\psi\rangle |\phi\rangle - |\phi\rangle|\psi\rangle \bigg) \bigg|^2 \\ &= \bigg| \dfrac{1}{2} \cdot 1 \cdot \bigg( |\psi\rangle |\phi \rangle + |\phi\rangle |\psi\rangle \bigg) + 0 \bigg|^2 \\ &= \dfrac{1}{4} \bigg| |\psi\rangle |\phi \rangle + |\phi\rangle |\psi\rangle \bigg|^2\\ &= \dfrac{1}{4} \big(\langle\psi| \langle\phi| + \langle\phi|\langle\psi| \big) \big( |\psi\rangle |\phi \rangle + |\phi\rangle |\psi\rangle \big) \\ &= \dfrac{1}{4} \bigg( 2 + 2\langle\psi|\langle\phi| \psi\rangle |\phi \rangle \bigg)\\ &= \dfrac{1}{4}\bigg(2 + 2\big| \langle \psi |\phi \rangle \big|^2 \bigg) = \dfrac{1}{2}\bigg(1 + \big| \langle \psi |\phi \rangle \big|^2 \bigg) \end{align}

Now, note that since

$$|\psi \rangle = \frac{|0\rangle_1 |\overrightarrow{x_i}\rangle_2 + |1\rangle_1|\overrightarrow{x_j}\rangle_2}{\sqrt 2}$$ $$|\phi \rangle = \frac{\|\overrightarrow{x_i}\| |0\rangle_1 - \|\overrightarrow{x_j}\| |1\rangle_1}{\sqrt Z}.$$

then we have

\begin{align} \langle \psi| \phi \rangle &= \dfrac{1}{\sqrt{2}\sqrt{Z}} \bigg( \langle 0 | 0 \rangle ||\overrightarrow{x_i}|| \ |\overrightarrow{x_i}\rangle_2 - 0 + 0 - \langle 1 | 1 \rangle ||\overrightarrow{x_j}|| \ |\overrightarrow{x_j}\rangle_2\bigg)\\ &= \dfrac{1}{\sqrt{2}\sqrt{Z}} \bigg( ||\overrightarrow{x_i}|| \ |\overrightarrow{x_i}\rangle_2 - ||\overrightarrow{x_j}|| \ |\overrightarrow{x_j}\rangle_2\bigg)\\ &= \dfrac{1}{\sqrt{2}\sqrt{Z}} \bigg( \overrightarrow{x_i} - \overrightarrow{x_j} \bigg)\\ \end{align}

The last equality is the way $|x_i \rangle$ is encoded, even though you didn't mentioned it, it should be $|x_i \rangle = \sum ||\overrightarrow{x_i}||^{-1} \ x_i |i\rangle $.

And therefore, $$ P(0) = \dfrac{1}{2}\bigg(1 + \big| \langle \psi |\phi \rangle \big|^2 \bigg) = \dfrac{1}{2}\bigg(1 + \bigg| \dfrac{1}{\sqrt{2}\sqrt{Z}} \big( \overrightarrow{x_i} - \overrightarrow{x_j} \big) \bigg|^2 \bigg) = \dfrac{1}{2}\bigg(1 + \dfrac{ \big| \overrightarrow{x_i} - \overrightarrow{x_j} \big|^2 }{2Z} \bigg)$$