How can we implement controlled-T gate using CNOT and H, S and T gates?

Question

In general, is there any way to implement a controlled version of an arbitrary gate U if we are given only CNOT and U gate?

Answer 1

You can use Toffolis and an ancilla to remove the need for the control on the T, then decompose the Toffolis into T+H+CNOT. Since the second Toffoli is uncomputing the ancilla, it can be replaced by a measurement based uncomputation.

Answer 2

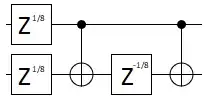
We can implement $CT$ using the following circuit:

This solutions uses an extra gate which isn't available above $R_I(\pi/8) = \sqrt{T}$

Explanation:

We know that $T = \sqrt{S} = Z^{\frac{1}{4}}$. Since $S,T,Z$ are all diagonal matrices hence their controlled versions will also be diagonal matrices $CZ,CS,CT$. Thus $CT=CZ^{\frac{1}{4}}$.

If we can implement the fourth root of $CZ$ using the above gates we will have a $Controlled-T$ gate.

We can implement a Controlled $Z$ gate using $CNOT$ and $H$ gates $$CZ = |0\rangle\langle 0|\otimes I + |1\rangle\langle 1|\otimes Z \\ = |0\rangle\langle 0|\otimes HIH + |1\rangle\langle 1|\otimes HXH \\ = (I\otimes H)(|0\rangle\langle 0|\otimes I + |1\rangle\langle 1|\otimes X)(I\otimes H)\\ = (I\otimes H)CNOT(I\otimes H)$$

We can implement $CNOT^{2t}$ gates using the circuit show in Craig Gidney's Answer

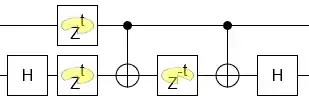
We need $CNOT^{1/4}$ hence $t=\frac{1}{8}$. This requires $Z^{\frac{1}{8}}$ i.e $R_{I}(\pi/8)$ and its Adjoint gate.

Let $U = (I\otimes H)CNOT^{\frac{1}{4}}(I\otimes H)$, then $$U^4= UUUU \\ = (I\otimes H)CNOT^{\frac{1}{4}}(I\otimes H) \times (I\otimes H)CNOT^{\frac{1}{4}}(I\otimes H) \times (I\otimes H)CNOT^{\frac{1}{4}}(I\otimes H) \times (I\otimes H)CNOT^{\frac{1}{4}}(I\otimes H) \\ = (I\otimes H)CNOT^{\frac{1}{4}}CNOT^{\frac{1}{4}}CNOT^{\frac{1}{4}}CNOT^{\frac{1}{4}}(I\otimes H) \\ = (I\otimes H)CNOT(I\otimes H) \\ = CZ$$ Thus $U = CZ^{\frac{1}{4}} = CT$

In general for implementing $Controlled-Z^{\frac{1}{2^n}}$ gate we would need $H$, $CNOT$ and $Z^{\frac{1}{2^{n+1}}}$(along with its adjoint version) gate.

Answer 3

In general you need more than $U$ and CNOT to implement a controlled-$U$. One approach to constructing a controlled-$U$ gate, for arbitrary $U \in \mathbf{U}(2)$, from single qubit and CNOT gates begins by parameterizing $U$ in terms of $U(\alpha,\beta,\gamma,\delta)$ according to $$U = e^{i\alpha}\begin{bmatrix} \exp\left({-i\frac{\beta+\delta}{2}}\right)\cos \frac{\gamma}{2} & -\exp\left({-i\frac{\beta-\delta}{2}}\right)\sin \frac{\gamma}{2} \\ \exp\left({i \frac{\beta-\delta}{2}}\right)\sin \frac{\gamma}{2} & \exp\left({i\frac{\beta+\delta}{2}}\right)\cos \frac{\gamma}{2} \end{bmatrix}.$$

With this parameterization, $U$ can be decomposed in terms of the Pauli matrices $\sigma_x, \, \sigma_y, \, \sigma_z$ as

$$U=e^{i\alpha}A \, \sigma_x B \, \sigma_x C, \;\;\; A \equiv e^{-\frac{i}{2}\beta \sigma_z}e^{-\frac{i}{4}\gamma \sigma_y}$$ $$B \equiv e^{\frac{i}{4}\gamma \sigma_y}e^{\frac{i}{4}(\beta+\delta) \sigma_z}, \;\;\; C\equiv e^{\frac{i}{4}(\beta-\delta) \sigma_z}.$$

The usefulness of this decomposition is that $U$ can be expressed as above, while $ABC=I$. Defining one additional gate $$D=\begin{bmatrix} 1 & 0 \\ 0 & e^{i \alpha} \end{bmatrix}$$ allows circuit implementation of an arbitrary controlled-$U$ using four single qubit gates and two CNOT gates as

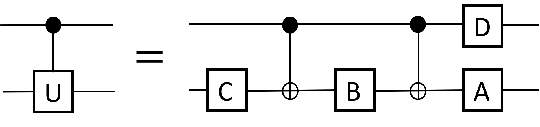
In the specific case noted in the title, $U=T$, the parameterization is $\alpha=\beta=\delta=\frac{\pi}{8}$, and $\gamma=0$. This gives $A=e^{-\frac{i \pi}{16} \sigma_z} \cong \sqrt{T} $, $B=e^{\frac{i \pi}{16} \sigma_z} \cong \sqrt{T^\dagger}$, $C=I$, $D=\sqrt{T}$ (where $\cong$ indicates equivalence up to global phase). It seems that you need access to $\sqrt{T}$ gates to implement the desired controlled-$T$.