I am a newbie to quantum machine learning. I am trying to build a quantum neural network (QNN). What I studied so far about QNN is that input would be qubits and hidden layer parameter can be set using rotation gates. Since we have limited qubits to use as in IBMQ (we can use 5 qubits only), I am unable to understand how the data set is inputed to our quantum circuit (QNN). If anyone can please guide me with that, would be great.
Thanks
There are many possible ways to encode data into a quantum neural network (QNN). In one of the first papers to suggest the use of variational circuits to classify data [1], the authors suggest the following general architecture for a QNN:
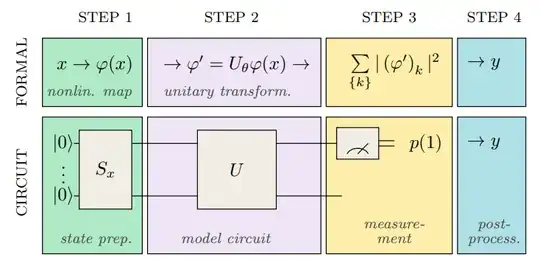
The circuit starts with the $|0\rangle$ state, encodes a data point $\textbf{x}$ using a circuit $S_\textbf{x}$, and transforms it using a parametrized unitary $U(\theta)$ (using rotations to encode parameters). The result of the classification is then given by the measurement of one of the qubit.
Now, what does the circuit $S_\textbf{x}$ look like? You have several possibilities, discussed and compared in a recent paper [2]. The two main ones are amplitude encoding and angle encoding.
Amplitude encoding (also called wavefunction encoding) consists in the following transformation:
$$ S_\textbf{x}|0\rangle=\frac{1}{||\textbf{x}||}\sum_{i=1}^{2^n} x_i |i\rangle $$
where each $x_i$ is a feature (component) of your data point $\textbf{x}$, and $\{|i\rangle\}$ is a basis of your $n$-qubit space (like $|0..00\rangle, |0..01\rangle,...,|1..11\rangle$). The advantage of this encoding is that you can store $2^n$ features using only $n$ qubits (so in the IBM case, 32 features). The disadvantage is that in general this circuit $S_{\textbf{x}}$ will have a depth of $O(2^n)$ and be very hard to construct.
Angle encoding (also called qubit encoding) consists in the following transformation:
$$ S_{\textbf{x}} |0\rangle=\bigotimes_{i=1}^n \cos(x_i)|0\rangle + \sin(x_i)|1\rangle. $$ It can be constructed using a single rotation with angle $x_i$ (normalized to be in $[-\pi,\pi]$) for each qubit, and can therefore encode $n$ features with $n$ qubits (so in your case only $5$ features). But it can be very easily constructed and has a depth of only 1. Note that there is a slight variant of this encoding, referred as dense angle encoding, that can encode $2n$ features in $n$ qubits $$ S_{\textbf{x}} |0\rangle=\bigotimes_{i=1}^n \cos(x_{2i-1})|0\rangle + e^{ix_{2i}}\sin(x_{2i-1})|1\rangle. $$ by using a phase gate after each rotation.
The question of what encoding you should use and which one can provide a quantum advantage is still an open research problem, since for the moment, there's no proof or empirical evidence that QNN are useful at all for machine learning tasks.
[1] Maria Schuld, Alex Bocharov, Krysta Svore and Nathan Wiebe, Circuit-centric quantum classifiers, 2018
[2] Ryan LaRose and Brian Coyle, Robust data encodings for quantum classifiers, 2020
