Very elementary proof of that Euler's totient function is multiplicative

Question

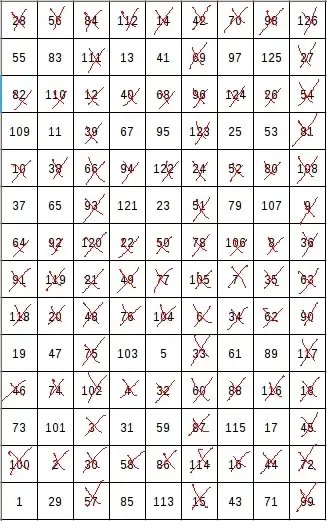
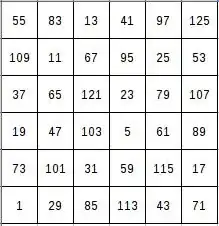
Well, I know two or three proofs of this fact $$\gcd(m,n)=1\implies \varphi(mn)=\varphi(m)\varphi(n)$$ where $\varphi$ is the totient function.

My problem is this: I'd like to explain this to some gifted children. The children are gifted enough to understand some basic facts, like the reason why $\varphi(n)$ is even ($k$ and $n$ are coprime $\iff$ $n-k$ and $k$ are, so make pairs) and they have a very solid intuitive idea of the Fundamental Theorem of Arithmetic (they know, for example, that if $a$ and $b$ are coprime, and $ab$ is a square, then both $a$ and $b$ are squares).

But I have tried to taught them why the totient function is multiplicative, but I (and they) understand that $\varphi$ is multiplicative but not an intuitive reason.

How would you explain it?

Answer 1

I would draw a $m \times n$ grid and fill it with numbers from $1$ to $mn$ like this: Start with a $1$ in the bottom-left square of the grid and keeping moving diagonally up and right, wrapping around the edges whenever you reach them.

Because $m$ and $n$ are coprime, all the numbers from $1$ to $mn$ will fit exactly in the grid with no overlap or empty square. This is a geometric interpretation of being coprime.

Now begin crossing out numbers that are not coprime to $mn$. One pattern that will emerge is, when a number is crossed out, either all the numbers in the same row are also crossed out, or all the numbers in the same column. This is because if you cross out a number $k$, then it either has a factor common with $m$ or with $n$. If it's $m$, then every other number in the same row will also be crossed out, since $\gcd(k,m)=\gcd(k\pm m,m)$. Similarly if $\gcd(k,n)\neq 1$, every other number in the same column is also crossed out.

Now if we remove all the crossed-out numbers we will get a rectangle consisting of $\phi(mn)$ squares. The width will be $\phi(n)$ and the height will be $\phi(m)$, so $\phi(mn)=\phi(m)\phi(n)$.

Here are the pictures for $m=14$, $n=9$.

Answer 2

Here's an intuitive but informal argument. For any fixed $n$, one has that $\frac{\varphi(n)}n$ is the probability that any arbitrarily chosen integer (uniformly in a very large interval) is relatively prime to$~n$. The multiplicativity of$~\varphi$ says that if $m,n$ have no common prime factors, then the events of being relatively prime to $m$ and to$~n$ are independent. It is easy to see that being divisible by one prime number is independent of being divisible by another prime number, and this can be generalised to the mutual independence of divisibility by any set of prime numbers. The multiplicativity of$~\varphi$ is now clear, because the sets of prime factors of $m,n$ are disjoint.

Of course making this into a formal argument requires proving the Chinese remainder theorem.

Answer 3

$\phi(n)$ is defined to be the number of integers in $\{1,\dots,n\}$ that are relative prime to $n$. Notice that $\{1,\dots,n\}$ is an arithmetic progression of length $n$ with common difference $1$. The key fact you should put forward is the following: $\phi(n)$ also equals the number of integers that are relatively prime to $n$ in any arithmetic progression $\{a+d,a+2d,\dots,a+nd\}$ of length $n$ - as long as the common difference $d$ is itself relatively prime to $n$.

Doing some examples should help this be intuitive: if $q$ is any divisor of $n$, then precisely every $q$th term in such an arithmetic progression will be a multiple of $q$, just like in the integers $\{1,\dots,n\}$. We might not know where the first occurrence is, but the number of occurrences is still $n/q$. And the overlaps with multiples of other divisors of $n$ are also exactly as numerous as they are in $\{1,\dots,n\}$. (In fact, working out the number of overlaps in $\{1,\dots,n\}$ is essentially using this key fact itself!)

With this key fact, here's the proof of the multiplicativity of $\phi(n)$. Let $\gcd(m,n)=1$. Partition $\{1,\dots,mn\}$ into $m$ arithmetic progressions of length $n$ and common difference $m$, say $\big\{ \{a,a+m,\dots,a+(n-1)m\} \colon 1\le a\le m \big\}$. Note that $\gcd(a+km,m) = \gcd(a,m)$; therefore exactly $\phi(m)$ of these arithmetic progressions are full of integers relatively prime to $m$, while the rest are full of integers not relatively prime to $m$. In each of the $\phi(m)$ "good" arithmetic progressions, exactly $\phi(n)$ integers are relatively prime to $n$ (using the above key fact and the aassumption $\gcd(m,n)=1$). Since an integer is relatively prime to $mn$ if and only if it's relatively prime to both $m$ and $n$, the total number of integers relatively prime to $mn$ is exactly $\phi(m)\phi(n)$, as desired.

Answer 4

I like Marc Van Leeuwens informal argument. I just would like to provide my interpretation of his injection. Euler's φ function can be described using probability: p(gcd(random num k<=n, n)=1) = φ(n)/n, φ(n) = n * p

You have two numbers, (n, m) st. gcd(n, m) = 1.

Set = {1, ..., nm} We ask ourselves: "If I pick a random number x within the set, what is the probability that it is relatively prime to nm"

Another way to ask this question is "If I pick a random number x within the set, what is the probability that is relatively prime to n and m." This is true because n and m share not factors, so in order for a number to be relatively prime to nm, it must be relatively prime to n and relatively prime to m.

p(gcd(x, nm)=1) = p(gcd(x, n)=1 and gcd(x, m)=1)

p(gcd(x, n)=1 and gcd(x, m)=1) = p(gcd(x, n)=1) * p(gcd(x, m)=1) because p(a and b) = p(a)*p(b)

   probability =    p(gcd(x, n)=1) *   p(gcd(x, m)=1) 
               =       (φ(n)/n)    *      (φ(m)/m)   
               = φ(n)φ(m)/(nm)

Final Conclusion:

   φ(nm) = p * nm = φ(n) * φ(m) 

I wonder if we can take this logic and extend it to when gcd(n, m) ≠ 1.

Answer 5

I don't think it is easy to explain to a child, there is what I would try (with some words and drawings, instead of formulas..)

• A little of sieving : $$n = \sum_{d | n} \sum_{k \le n} 1_{gcd(k,n) = d} = \sum_{d | n} \sum_{k \le n/d} 1_{gcd(k,n) = 1} = \sum_{d | n} \varphi(n/d)$$

• Let $gcd(n,m) = 1$ and $\varphi(ab)=\varphi(a)\varphi(b)$ for every $a|n,b |m$ other than $ab = nm$, you get $$nm = \sum_{d | nm}\varphi(d)=\sum_{a | n}\sum_{b | m} \varphi(ab)$$ $$ = \varphi(nm)-\varphi(n)\varphi(m)+ \sum_{a|n}\varphi(a)\sum_{b|n}\varphi(b)$$ $$ = \varphi(nm)-\varphi(n)\varphi(m)+nm$$