On finding the equilibrium solutions to a system of differential equations

Question

I am asked to find all equilibrium solutions to this system of differential equations:

$$\begin{cases} x ' = x^2 + y^2 - 1 \\ y'= x^2 - y^2 \end{cases} $$

and to determine if they are stable, asymptotically stable or unstable.

I do not know how to proceed, I tried switching to polar coordinates to make the system linear in some way but I did not succeed.

Would I need to use a software to solve this?

Context: I am following the course of Arthur Mattuck (MIT opencourseware), but I can't seem to find these type of systems, or equilibrium points.

Answer 1

This answer posted in response to the modified system, given in (1) and (2) below:

Oy Gevalt! NOW there is work!

Where is Moshe now that we need him to lead us out from under Pharoah's toil?

Well, I ain't no $Moshe$ but I can cut some down some of the work, thus:

The system to be considered is now

$x' = x^2 + y^2 - 1, \tag{1}$

$y' = x^2 - y^2; \tag{2}$

the number of equilibria has jumped from none to four! To see this, note that now $x' = y' = 0$ implies, from (1), (2), that

$x^2 + y^2 = 1, \tag{3}$

$x^2 = y^2; \tag{4}$

using (4) in (3) yields

$2x^2 = 1 \Rightarrow x = \pm \dfrac{\sqrt 2}{2}; \tag{5}$

we see from (4) that $y$ may take the same values; the equilibria occur at the four points

$(x, y) = (\pm \dfrac{\sqrt 2}{2}, \pm \dfrac{\sqrt 2}{2}). \tag{6}$

It may also be seen, geoemtrically, that the equilibria are given by (6), since (3) is the equation of a circle, centered at the origin and of radius $1$, and (4) is the combined equation of the two lines $x \pm y = 0$, since

$x^2 = y^2 \Rightarrow x = \pm y \Rightarrow x \pm y = 0; \tag{7}$

the circle intersects these lines at the specified points (6). In any event, having the equilibria of the system (1)-(2) at hand, the next step is to linearize the equations about these four points, and see what we get. Linearizing requires computation of the Jacobian matrix $J(x, y)$ of the vector field $(x', y')^T = (x^2 + y^2 -1, x^2 - y^2)^T$; we have

$J(x, y) = \begin{bmatrix} \dfrac{\partial x'}{\partial x} & \dfrac{\partial x'}{\partial y} \\ \dfrac{\partial y'}{\partial x} & \dfrac{\partial y'}{\partial y} \end{bmatrix} = \begin{bmatrix} 2x & 2y \\ 2x & -2y \end{bmatrix} = 2\begin{bmatrix} x & y \\ x & -y \end{bmatrix}, \tag{8}$

and we next must evaluate and eigen-analyze $J(\pm \dfrac{\sqrt{2}}{2}, \pm \dfrac{\sqrt{2}}{2})$ for all four possible combinations of $\pm \dfrac{\sqrt{2}}{2}$, i.e., at all four points $(\pm \dfrac{\sqrt{2}}{2}, \pm \dfrac{\sqrt{2}}{2})$. Well, some the the Oy! Gevalt! can be mollified by lessening the amount of work by realizing that, due to certain symmetries of the problem, there are really only two matrices $J(x, y)$ which need to be considered, not four. This is most easily seen by breaking the situation up into quadrants:

$J(-\dfrac{\sqrt{2}}{2}, -\dfrac{\sqrt{2}}{2}) = -J(\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}), \; \; \text{for quadrants I, III}, \tag{9}$

$J(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}) = -J(\dfrac{\sqrt{2}}{2}, -\dfrac{\sqrt{2}}{2}), \; \; \text{for quadrants II, IV}; \tag{10}$

in this way we only need perform the eigen-analysis on two matrices out of the four $J(\pm \dfrac{\sqrt{2}}{2}, \pm \dfrac{\sqrt{2}}{2})$, so lets start with $J_I = J(\dfrac {\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2})$; its characteristic polynomial, call it $p_I(\lambda)$, is

$p_I(\lambda) = \det (\begin{bmatrix} \sqrt{2} - \lambda & \sqrt{2} \\ \sqrt{2} & -\sqrt{2} - \lambda \end{bmatrix}) = \lambda^2 - 4. \tag{11}$

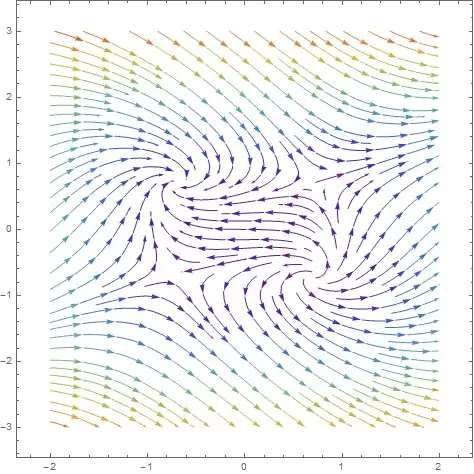
We see from (11) that the eigenvalues of $J_I$ are $\lambda = \pm 2$; since $J_I$ has a positive eigenvalue, the point $(\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2})$ is unstable; since $J_I$ also has a negative eigenvalue, this point is a saddle; by (9), $J_{III} = -J_I$ also has eigenvalues $\pm 2$, and hence also unstable and a saddle. These facts are borne out by the excellent graphic contributed by Amzoti in his answer. We next turn to $J_{II}$; since we are now in the second quadrant, we have

$J_{II} = J(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}) = \begin{bmatrix} -\sqrt{2} & \sqrt{2} \\ -\sqrt{2} & -\sqrt{2}\end{bmatrix}, \tag{12}$

$p_{II}(\lambda) = \det(J_{II} - \lambda I) = \det(\begin{bmatrix} -\sqrt{2} - \lambda & \sqrt{2} \\ -\sqrt{2} & -\sqrt{2} - \lambda \end{bmatrix})$ $= (\lambda + \sqrt{2})^2 + 2 = \lambda^2 + 2\sqrt{2} \lambda + 4; \tag{13}$

the zeroes of $p_{II}(\lambda)$ are found via the quadratic formula:

$\lambda = \dfrac{1}{2}(-2\sqrt{2} \pm \sqrt{8 - 16}) = \dfrac{1}{2}(-2\sqrt{2} \pm 2i\sqrt{2}) = -\sqrt{2} \pm i\sqrt{2}; \tag{14}$

we we see that the eigenvalues of $J_{II}$ are not real, but have negative real part; thus $(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2})$ is a stable spiral. Furthermore, since $J_{IV} = -J_{II}$, the eigevalues of $J_{IV}$ are $\lambda = \sqrt{2} \pm i\sqrt{2}$; thus the point $(-\dfrac{\sqrt{2}}{2}, -\dfrac{\sqrt{2}}{2})$ is an unstable spiral. All these computations support and are supported by Amzoti's grahic of the phase portrait of (1)-(2).

The stable spiral point at $(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2})$ is in fact asymptotically stable; this follows from the fact that $\Re(\lambda) < 0$ for each of the eigenvalues of $J_{II}$; this fact is both well-known and well documented, for example in the excellent reference provided by Amzoti in his comment.

There appears to be a discrepancy in the calculation of eigenvalues by Monolinte and myself, but we agree on the qualitative features of the equilibrium points. As ever, abstract analysis is easy but arithmetic proves difficult! Until further notice, I'm standing by my calculations.

Hope this helps! Cheers,

and as ever,

Fiat Lux!!!

Answer 2

This answer posted in response to the original system, given in (1) and (2) below:

The equilibrium solutions occur at those values of $(x, y) \in \Bbb R^2$ at which $x' = y^\prime = 0$; thus from

$x' = x^2 + y^2 + 1, \tag{1}$

$y' = x^2 - y^2, \tag{2}$

we see that there are no points $(x, y)$ for which $x^\prime = 0$; $x^2 + y^2 + 1$ has no real zeroes, being strictly positive (in fact, $\ge 1$) everywhere.

We conclude the system has no equilibrium solutions; we are in luck, since now we are spared the work of analyzing their stability!

Hope this helps. Cheers,

and as always,

Fiat Lux!!!

Answer 3

We are given:

$$\begin{cases} x ' = x^2 + y^2 - 1 \\ y'= x^2 - y^2 \end{cases} $$

As @RobertLewis has pointed out, we find the equilibrium points $(x,y)$ at the points where we have $x' = y' = 0$. We have

$x^2 + y^2 -1 =0\, \tag{3}$

$x^2 - y^2 = 0. \tag{4}$

From $(4)$, we have $x^2 = y^2$. Substituting this back into $(3)$, yields $x=\pm \dfrac{1}{\sqrt{2}}$. We can substitute this $x$ back into $(4)$, yielding $y = \pm \dfrac{1}{\sqrt{2}}$. Thus, we have a total of critical points as:

$$(x, y) = \left(-\dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}}\right), \left(-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right), \left(\dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}}\right), \left(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right)$$

You should validate that each of these four points gives you $x'= y' = 0$ by substituting them into the original system.

Your next step is to use linearization, find the Jacobian and evaluate the eigenvalues for those four critical points to determine stability. I am going to let you work that, but here are some nice notes with a summary, the gotchas with linearzation and examples (starts on page $4$). I am also not sure if you discussed nullclines, but the notes have those also and they can be superimposed on the phase portrait. Hint: there are three unstable and one stable critical point.

Here is a phase-portrait for the system showing the four critical points (which can be used to validate your critical points and stability analysis).

Answer 4

Continuing from where Amzoti left (by the way thanks).

Using the dot notation for derivatives.

The Jacobian of the system is: $$J(x, y) = \begin{bmatrix} \dfrac{\partial {\dot x}}{\partial x} & \dfrac{\partial {\dot x}}{\partial y} \\ \dfrac{\partial {\dot y}}{\partial x} & \dfrac{\partial {\dot y}}{\partial y} \end{bmatrix} = \begin{bmatrix} 2x & 2y \\ 2x & -2y \end{bmatrix}; $$

I find the eigenvalues at the solution $(\sqrt{\frac{1}{2}};\sqrt{\frac{1}{2}})$, i.e., I solve this equation (by definition of eigenvalue): $$\begin{vmatrix} \lambda -2\sqrt{\frac{1}{2}} & 2\sqrt{\frac{1}{2}} \\ 2\sqrt{\frac{1}{2}} & \lambda+2\sqrt{\frac{1}{2}} \end{vmatrix} = 0$$

$$\begin{vmatrix} \lambda -2\sqrt{\frac{1}{2}} & 2\sqrt{\frac{1}{2}} \\ 2\sqrt{\frac{1}{2}} & \lambda+2\sqrt{\frac{1}{2}} \end{vmatrix} = \lambda^2 -4$$

so the eigenvalues are $\lambda_1 = +2 \ ; \lambda_2 = -2.$ When the eigenvalues are real numbers with different sign the equilibrium point is a saddle that is unstable.

I repeat the process for the other equilibrium solutions and obtain for $$(\sqrt{\frac{1}{2}};-\sqrt{\frac{1}{2}}), \lambda_1=2\sqrt{\frac{1}{2}}-2i; \ \lambda_2=\sqrt{\frac{1}{2}}+2i \tag{1}$$ $$(-\sqrt{\frac{1}{2}};+\sqrt{\frac{1}{2}}), \lambda_1=-2\sqrt{\frac{1}{2}}-2i; \ \lambda_2=-\sqrt{\frac{1}{2}}+2i \tag{2}$$ $$(-\sqrt{\frac{1}{2}};-\sqrt{\frac{1}{2}}), \lambda_1=2; \ \lambda_2=-2 \tag{3}$$ In $(1)$real parts are both positive so I have a repellor point that is unstable.

In $(2)$real parts are both negative so I have an attractor point that is stable.

In $(3)$ we have the saddle case again, unstable.

Now I am only left with the asymptotically stable cases, anybody mind lending a hand?