Prove Existence of a Circle

Question

There are two circles with radius $1$, $c_{A}$ and ${c}_{B}$. They intersect at two points $U$ and $V$. $A$ and $B$ are two regular $n$-gons such that $n > 3$, which are inscribed into $c_{A}$ and ${c}_{B}$ so that $U$ and $V$ are vertices of $A$ and $B$.

Then suppose a third circle, $c$, with a radius of $1$ is to be placed so that it intersects $A$ at two of its vertices $W$ and $X$ and intersects $B$ at two of its vertices $Y$ and $Z$.

Details and Assumptions:

1. Assume that $U,V,W,X,Y,Z$ are all distinct points.

2. $U$ lies outside of $c$.

3. $V$ lies inside of $c$.

Given all of these details, prove that there exists a regular $2n$-gon which comprises of $W,X,Y,Z$ as its 4 vertices.

Answer 1

This answer focuses on identifying families of solutions to the problem described in the question.

I've made two provisional conjectures in order to make progress with the problem:

1. The result can be stated for three $2n$-gons rather than two $n$-gons and one $2n$-gon.

2. Solutions have mirror symmetry. Or equivalently, in any solution there are two pairs of $2n$-gons which have the same degree of overlap. [This turns out to be false - see 'Solution family 5' below. However, this condition is assumed in Solution families 1-4.]

[Continuation 6: in an overhaul of the notation I've halved $\phi$ and doubled $m$ so that $m$ is always an integer.]

If we define the degree of overlap, $j$, between two $2n$-gons $(n>3)$ as the number of edges of one that lie wholly inside the other, then $1 < j < n$.

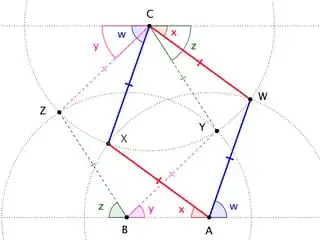
If $$ \phi = \frac{\pi}{2n} $$ is half the angle subtended at the centre of the $2n$-gon by one of its edges, then the distance between the centres of two overlapping $2n$-gons is $$ D_{jn} = 2\cos{j\phi} $$ Consider a $2n$-gon P which overlaps a $2n$-gon O with degree $j$. Now bring in a third $2n$-gon, Q, which also overlaps O with degree $j$ but is rotated about the centre of O by an angle $m\phi$ with respect to P, where $m$ is an integer.

The distance between the centres of P and Q, which I'll denote by $D_{kn}$ for a reason that will become apparent, is $$ D_{kn} = 2D_{jn}\sin{\tfrac{m}{2}\phi} = 4\cos{j\phi} \, \sin{\tfrac{m}{2}\phi} $$

We now demand that P and Q should overlap by an integer degree, $k$, so that $$ D_{kn} = 2\cos{k\phi} $$ This will ensure that all points of intersection coincide with vertices of the intersecting polygons, and thus provide a configuration satisfying the requirements of the question (with the proviso that the condition does not guarantee that there is a common area of overlap shared by all three polygons).

We have omitted mention of the orientation of the polygons, but it is easily shown that this is always such as to achieve the desired overlap.

Combining the two expressions for $D_{kn}$ gives the condition

$$ 2\cos{j\phi}\, \sin{\tfrac{m}{2}\phi} = \cos{k\phi} $$ or (since $n\phi=\pi/2$) $$ 2\cos{j\phi}\, \cos{(n-\tfrac{m}{2})\phi} = \cos{k\phi} \tag{1} $$

The configurations we seek are solutions of this equation for integer $n$, $j$, $k$ and $m$.

In the first example in the question $n = 12, j = 8, k = 6, m = 12$.

In the second example $n = 15, j = 6, k = 10, m = 6$.

[Continuation 6: for solutions under the constraint of conjecture 2, $m$ is always even, but in the more general case $m$ may be odd.]

I'll now throw this open to see if anyone can provide a general solution. It seems likely that $j$, $k$ and $m/2$ must be divisors of $2n$ [this turns out to be incorrect], and I have a hunch that the solution will involve cyclotomic polynomials [this turns out to be correct].

---

Continuation (1)

I've now identified 3 families of solutions consistent with conjecture 2 (mirror symmetry), all involving angles of 60 degrees. There may be others.

Solution family 1

This family is defined by setting $j=2n/3$. This means that half the angle subtended at the centre of O by its overlapping edges is $\tfrac{\pi}{3}$ radians or 60 degrees. Since $\cos{\tfrac{\pi}{3}} = \tfrac{1}{2}$ it reduces equation 1 to $$ \cos{(n-\tfrac{m}{2})\phi} = \cos{k\phi} $$ so there are solutions with $$ n-\tfrac{m}{2} = k $$ (where $\tfrac{m}{2}$ is an integer) subject to $2 \le k \le n-1\,\,$, $1 \le \tfrac{m}{2} \le n-2\,\,$ and $3|n$.

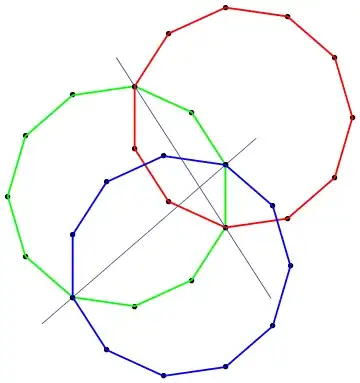
The first example in the question belongs to this family. The complete set of solutions for $n=12$ combine to make this pleasing diagram:

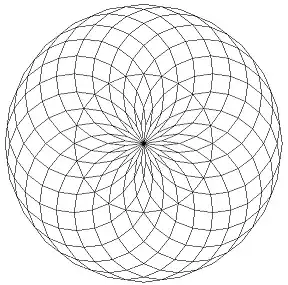
Solution family 2

This family has $m=2n/3$. This makes $\cos{(n-\tfrac{m}{2})\phi}=\cos{(\pi/3)} = \tfrac{1}{2}$, which reduces equation 1 to $$ \cos{j\phi} = \cos{k\phi} $$ so (given that $j<n$ and $k<n$) $$ j = k $$ These solutions have threefold rotational symmetry. The only restriction is that $n$ must be divisible by 3. Example ($n=9, j=k=4, m=6$):

Solution family 3

This family is the most interesting of the three, but yields only one solution. It is defined by setting $k=2n/3$ so that $\cos{k\phi}=\cos{\tfrac{\pi}{3}} = \tfrac{1}{2}$. Equation 1 then becomes

$$ 2\cos{j\phi}\,\cos{(n-\tfrac{m}{2})\phi} = \tfrac{1}{2} $$ which may be written in the following equivalent forms: $$ \cos{(n+\tfrac{m}{2}-j)\phi} + \cos{(n+\tfrac{m}{2}+j)\phi} = -\tfrac{1}{2} \tag{2} $$ $$ \cos{(n-\tfrac{m}{2}-j)\phi} + \cos{(n-\tfrac{m}{2}+j)\phi} = \tfrac{1}{2} \tag{3} $$ Solutions to these equations can be found using the following theorem relating the roots $z_i(N)$ of the $N$th cyclotomic polynomial to the Möbius function $\mu(N)$:

$$ \sum_{i=1}^{\varphi(N)} {z_i(N)} = \mu(N) $$ where $\varphi(N)$ is the Euler totient function (the number of positive integers less than $N$ that are relatively prime to $N$) and $z_i(N)$ are a subset of the $N$th roots of unity. Taking the real part of both sides and using symmetry this becomes: $$ \sum_{i=1}^{\varphi(N)/2} { \cos{(p_i(N) \frac{2\pi}{N})} } = \tfrac{1}{2} \mu(N) \tag{4} $$ where $p_i(N)$ is the $i$th integer which is coprime with $N$.

The Möbius function $\mu(N)$ takes values as follows:

$\mu(N) = 1$ if $N$ is a square-free positive integer with an even number of prime factors.

$\mu(N) = −1$ if $N$ is a square-free positive integer with an odd number of prime factors.

$\mu(N) = 0$ if $N$ has a squared prime factor.

Equation 4 thus provides solutions to equations 2 and 3 if $\varphi(N) = 4$, $\mu(N)$ has the appropriate sign and the cosine arguments are matched.

The first two conditions are true for only two integers:

$N=5$, with $\mu(5)=-1$, $p_1(5) = 1, p_2(5) = 2$

$N=10$, with $\mu(10)=1$, $p_1(10) = 1, p_2(10) = 3$.

We first set $N=5$ and look for solutions to equation 2.

Matching the cosine arguments requires firstly that $$ 2j \frac{\pi}{2n} = (p_2(5)-p_1(5))\frac{2\pi}{5} $$ from which it follows that $$ 5j = 2n $$

$n$ must be divisible by 3 to satisfy $k=2n/3$, so the smallest value of $n$ for which solutions are possible is $n=15$, with $k=10$ and $j=6$. All other solutions will be multiples of this one. Matching the cosine arguments also requires that $$ (n+\tfrac{m}{2}-j) \frac{\pi}{2n} = p_1(5) \frac{2\pi}{5} $$ which implies $m=6$.

This is the solution illustrated by the second example in the question.

Setting $N=10$ and looking for solutions to equation 3 yields the same solution.

---

Continuation (2)

Solution family 4

A fourth family of solutions can be obtained by writing equation 1 as

$$ \cos{(n+\tfrac{m}{2}-j)\phi} + \cos{(n+\tfrac{m}{2}+j)\phi} + \cos{k\phi} = 0 \tag{5} $$

and viewing this as an instance of equation 4 with $\varphi(N)/2 = 3$ and $\mu(N) = 0$. There are two values of N which satisfy these conditions, $N = 9$ and $N = 18$, which lead to three solutions:

For $N = 9$: $$ n=9, j=6, k=8, m=2 \\n=9, j=4, k=4, m=6 $$

For $N=18$: $$ n=9, j=2, k=2, m=6 $$

However, these are not new solutions. The first is a member of family 1 and the last two are members of family 2.

---

Continuation (3)

Solution family 5

Rotating a $2n$-gon about a vertex by an angle $m\phi$ moves its centre by a distance $$ 2\sin{ \tfrac{m}{2}\phi} = 2\cos{(n-\tfrac{m}{2})\phi} = D_{n-m/2,n}. $$ If $m$ is even the rotated $2n$-gon thus overlaps the original $2n$-gon with integer degree $n-\tfrac{m}{2}$, and a third $2n$-gon with a different $m$ may overlap both of these, providing another type of solution to the problem.

Solutions of this kind may be constructed for all $n \ge 3$. The diagram below includes the complete set of such solutions for $n=5$. A similar diagram with $n=12$ (but with a centrally placed $2n$-gon of the same size which can only be added when $3|n$) is shown above under Solution family 1.

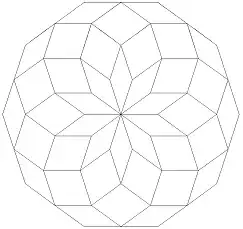
This family of solutions provides exceptions to conjecture 2: not all groups of three $2n$-gons overlapping in this way show mirror symmetry.

---

Continuation (4)

If we relax the condition set by conjecture 2, allowing solutions without mirror symmetry, we need an additional parameter, $l$, to specify the degree of overlap between O and P (which is now no longer $j$).

The distances between the centres of the three $2n$-gons are now related by the cosine rule:

$$ D_{nk}^2 = D_{nj}^2 + D_{nl}^2 - 2 D_{nj}D_{nl}\cos{m_k\phi}, $$ where a subscript $k$ has been added to $m$ to acknowledge the fact that $j$, $l$ and $k$ can be cycled to generate three equations of this form. These can be written $$ \\ \cos^2{J} + \cos^2{L} - 2 \cos{J} \cos{L} \cos{M_k} = \cos^2{K} \\ \cos^2{K} + \cos^2{J} - 2 \cos{K} \cos{J} \cos{M_l} = \cos^2{L} \\ \cos^2{L} + \cos^2{K} - 2 \cos{L} \cos{K} \cos{M_j} = \cos^2{J} $$ where $$ J = j\phi,\, L = l\phi,\, K = k\phi, \\M_j = m_j\phi,\, M_l = m_l\phi,\, M_k = m_k\phi $$

The same result in a slightly different form is derived in the answer provided by @marco trevi.

$M_j$, $M_l$ and $M_k$ are the angles of the triangle formed by the centres of the three polygons. Since these sum to $\pi$ we have $$ m_j + m_l + m_k = 2n $$

The sine rule gives another set of relations: $$ \frac{\cos{J}}{\sin{M_j}} = \frac{\cos{L}} {\sin{M_l}} = \frac{\cos{K}}{\sin{M_k}} $$

In general the $m$ parameters are limited to integer values (as can be seen by considering the symmetry of the overlap between a $2n$-gon and each of its two neighbours). But they are now not necessarily even.

Answer 2

Answering the easier question about why the points always lie on a regular $2n$-gon. Leaving the more interesting question about listing the possible values of $n$ when this may happen for later (or for somebody else!).

---

Let us denote $\phi=2\pi/n$. We align the coordinate axes in such a way that the center of $c_A$ is at the origin $O$ and that the positive $x$-axis intersects $c_A$ at a vertex of of $A$. This implies that the points $U,V,X,W$ all have angular polar coordinates that are integer multiples of $\phi$.

Let $L_1$ (resp. $L_2$) be the line through $U$ and $V$ (resp. through $W$ and $X$). The line $L_1$ is perpendicular to the bisector of the angle between $\vec{OU}$ and $\vec{OV}$. Therefore $L_1$ points at the direction that is perpendicular to an integer multiple of $\phi/2$. The same holds for $L_2$. Thus the angle $\theta$ between $L_1$ and $L_2$ is also an integer multiple of $\phi/2$, so $\theta= k\pi/n$ for some integer $k$.

Let $s_1$ (resp. $s_2$) be the reflection w.r.t. $L_1$ (resp. $L_2$). It is well known that the composition $r=s_2\circ s_1$ is a rotation about the point of intersection $Q=L_1\cap L_2$ by the angle $2\theta=2k\pi/n=k\phi$. If this is news to you the animation below may make this clearer. There the black arrow is first reflected w.r.t. the blue line, and the red arrow is the mirror image. For its part the red arrow is then reflected w.r.t. the green line and the orange arrow is its mirror image. The animation tries to convince you that irrespective of which direction the black arrow points at, the angle between it and the red orange arrow is constant (=twice the angle between the blue and green lines). Prove this if you already haven't. It's not difficult!

It is clear that $A=s_1(B)$ and that the $s_2(A)=r(B)$ is a regular $n$-gon circumscribed by $c$. This implies that $r(c_B)=c$. Also, as the angle of rotation $2\theta$ is a multiple of $\phi$, the sides of the regular $n$-gon $r(B)$ are parallel to those of $B$. The figure below hopefully makes it clearer what happened. After we reflected $n$-gon $B$ (red) first w.r.t. line $L_1$ to get the $n$-gon $A$ (green) and then w.r.t. line $L_2$ the resulting $n$-gon (blue) can be gotten from $B$ also by a parallel translation. Quite irrespective of whether the circles $c_B$ and $c$ intersect on vertices of the $n$-gon $B$ or not (in the image they intentionally do not)!

Let $s_3$ is the reflection w.r.t. the line $L_3$ passing through $Y$ and $Z$. If $O_B$ is the center of the circle $c_B$, then the angle $\beta=\angle YO_BZ$ is an integer multiple of $\phi$, say $\beta=\ell\phi$. The angle between $YZ$ and $O_BY$ is thus $$\gamma=\frac\pi2-\frac\beta2=\frac\pi2-\frac{\ell\pi}n=\frac\pi{2n}(n-2\ell).$$ This means that the angle between $L_3$ and the extension of any edge of $B$ is an integer multiple of $\pi/2n=\phi/4$. Thus, under the reflection $s_3$ the directions of those edges change by an integer multiple of $\phi/2$. Therefore the regular $n$-gon $s_3(B)$ is either parallel to $r(B)$ itself or parallel to a version rotated by $\phi/2$ (depending on the parity of $n-2\ell\equiv n\pmod2$). Because $s_3(B)=s_3(s_1(A))$ the $n$-gons $s_3(B)$ and $A$ are parallel. With a little imagination you see in the above figure that the green 11-gon is "half a tick" off synch from the blue and red 11-gons that are parallel to each other.

As both regular $n$-gons, $s_3(B)$ and $r(B)$ are circumscribed by $c$, $r(B)$ contains $W$ and $X$ as vertices, and $s_3(B)$ contains $Y$ and $Z$ as its vertices, the claim follows from this.

---

Extras that may or may not help in simplifying the above argument or finding the solutions:

Because we get $c$ by rotating $c_B$ about $Q$, the point $Q$ must be equidistant from the centers of $c_B$ and $c$. In other words, $Q$ is on the line $YZ$ (so the lines $L_1$, $L_2$ and $L_3$ intersect at the same point $Q$).

Recalling that $s_3$ is the reflection w.r.t. $YZ$, then $s_3\circ r$ is yet another reflection (as an orientation reversing rigid motion of the plane), call it $s_4$. Clearly $s_4(Q)=Q$ and $s_4(c_B)=c_B$, so $s_4$ must be the reflection w.r.t. line joining $Q$ and the center of $c_B$.

Answer 3

I tried to solve the problem in a more general setting. However, despite my (hard!) effort this is NOT an answer. The reason I am posting it here is because it might shed some further light on this problem and on its general version, which I find very entertaining and interesting. So, if my reasoning could help someone find a nice solution, here it is.

Let $A_m$ and $A_n$ be two regular polygons of $m$ and $n$ sides respectively, each inscribed in a circle of radius $1$. Let's say that they "fit together to order $d$" (invented notation) if $d$ divides both $m$ and $n$.

This corresponds visually to putting the polygons one over the other in such a way that the centers of the corrisponding circumscribed circles coincide and letting one of the vertices of one polygon coincide with a vertex of the other one. Then $d$ is the number of vertices in the picture which belong to both polygons.

The possible "fitting orders" for $A_m$ and $A_n$ are then $1=d_1,d_2,d_3,\dots,d_r=\gcd(m,n)$ where the $d_i$'s are all common divisors of $m$ and $n$. Let's denote this set as $D_{m,n}$.

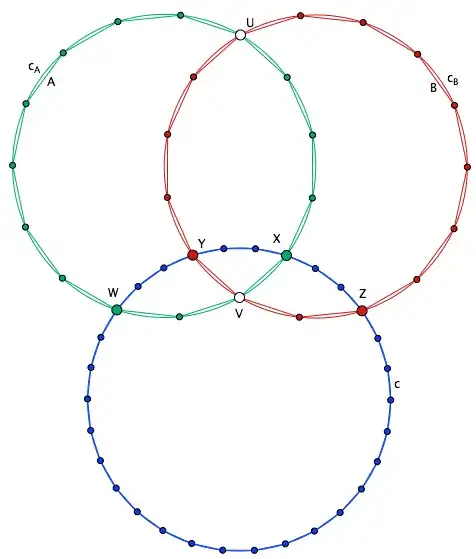
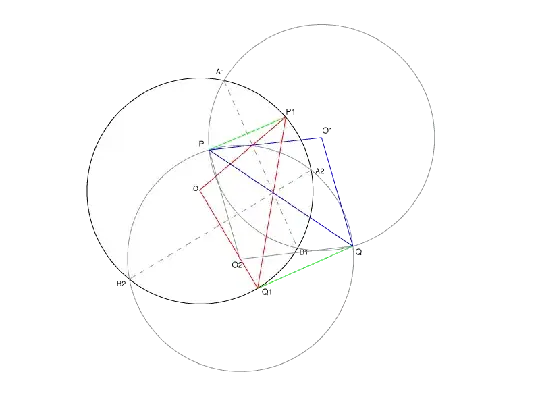
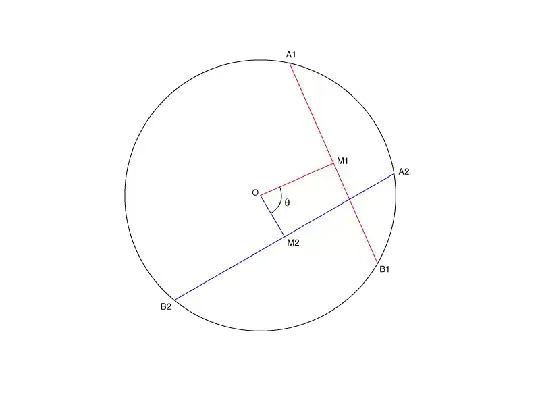Now, for the geometrical setting, let's take a circle $C$ with radius $1$ and center $O$ and two chords $\overline{A_1B}_1$ and $\overline{A_2B}_2$. Let $M_1$ and $M_2$ be the midpoint of $\overline{A_1B}_1$, resp. $\overline{A_2B}_2$, and let $\theta$ be the angle $M_1\widehat{O}M_2$, as in the picture below: Reflecting $C$ about $\overline{A_1B}_1$ gives another circle $C_1$; doing the same with $\overline{A_2B}_2$ gives a circle $C_2$. These circles might or might not intersect; let's suppose they do. Then they will meet at two points $P$ and $Q$. 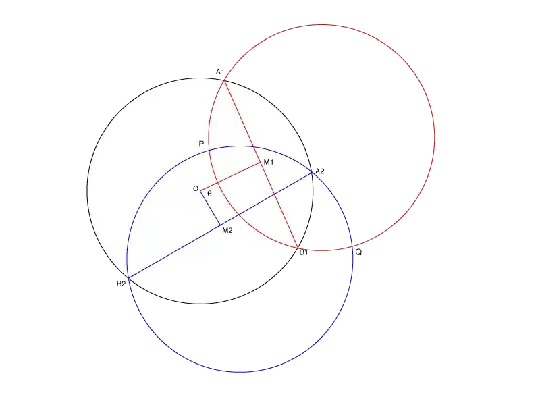Reflecting $P$ about the two chords, we get two points $P_1$ and $P_2$ which lay on the original circle $C$. Doing the same with $Q$, we get two other points $Q_1$ and $Q_2$. By symmetry, one can see that $\overline{PQ}=\overline{P_1Q}_1=\overline{P_2Q}_2$ and also $P\widehat{O}_1Q=P\widehat{O}_2Q=P_1\widehat{O}Q_1=P_2\widehat{O}Q_2$, where $O_1$ and $O_2$ are the centers of $C_1$ and $C_2$. Here's the picture for $P_1$ and $Q_1$:

So, we started with two chords on a circle and ended up with two other chords of equal length in some random position on the circle. Getting back to polygons, given three polygons $A_m,A_n$ and $A_p$ we can choose two chords of $A_m$ (i.e. segments whose endpoints are vertices of the polygon) by selecting $d_1\in D_{m,n}$ and $d_2\in D_{m,p}$ and by deciding what is their position on the polygon. This choice will determine two other chords which, in general will be chords of the circumscribed circle of $A_m$ but not of $A_m$ itself;

the challenge is determining what values of $n$ and $p$ lead to chords which are also chords of $A_m$. A necessary condition for this is that the angle $P\widehat{O}_1Q$ must be of the form $2\pi/d^*$ where $d^*$ is a common divisor to $m,n$ and $p$. This angle $\alpha^*$ is uniquely determined by the distance $\overline{O_1O_2}=L$, because $L/2=\cos(\alpha^*/2)$. On the other side, we have (by the law of cosines) \begin{equation} L^2=\overline{OO}_1^2+\overline{OO}_2^2-2\overline{OO}_1\ \overline{OO}_2\cos\theta \end{equation} But we have also \begin{equation} \overline{OO}_1=2\cos\left(\frac{\pi}{d_1}\right)\qquad \overline{OO}_2=2\cos\left(\frac{\pi}{d_2}\right) \end{equation} so \begin{equation} (L/2)^2=\cos^2(\pi/d_1)+\cos^2(\pi/d_2)-2\cos(\pi/d_1)\cos(\pi/d_2)\cos\theta= \cos^2(\pi/d^*) \end{equation} We have that $\theta$ as well has to be a multiple of $2\pi/m$, so we can set $\theta = 2\pi/d$ with $d$ divisor of $m$.

In the end the problem is finding $d_1,d_2,d^*$ and $d$ such that \begin{equation} \cos^2(\pi/d_1)+\cos^2(\pi/d_2)-2\cos(\pi/d_1)\cos(\pi/d_2)\cos(\pi/d)= \cos^2(\pi/d^*) \end{equation}

This will yeld all the possible combinations of three polygons which will "fit together" in some way. I don't know how to solve this, but I thought to share it with you in case someone could see the solution.

Answer 4

Here's a straightforward proof of the existence of the $2n$-gon.

Ignoring polygons for the time being, take points $W$ and $X$ on $\bigcirc A$ and points $Y$ and $Z$ on $\bigcirc B$, such that $W$, $X$, $Y$, $Z$ all lie on $\bigcirc C$, where all three circles are congruent.

Define $w$, $x$, $y$, $z$ to be the measures of angles made, respectively, by radial segments $\overline{AW}$, $\overline{AX}$, $\overline{BY}$, $\overline{BZ}$ with $\overleftrightarrow{AB}$. (These four measures, as described, are ambiguous; that's okay.) Because $\square AWCX$ and $\square BYCZ$ are rhombi —and therefore also parallelograms— radial segments $\overline{CX}$, $\overline{CW}$, $\overline{CZ}$, $\overline{CY}$ make comparable angles with the line through $C$ parallel to $\overleftrightarrow{AB}$.

Clearly, then, the measure of any $\angle PCQ$, with $P$ and $Q$ in $\{W, X, Y, Z\}$, is some combination of $\pm w$, $\pm x$, $\pm y$, $\pm z$, and $\pm \pi$. (Allowing $\pm \pi$ eliminates any problems with our ambiguously-defined $w$, $x$, $y$, $z$.) Most importantly: If $w$, $x$, $y$, $z$, $\pi$ are multiples of a common value, then those $\angle PCQ$s will be, as well.

Recalling the original context of the problem, we have that $\bigcirc A$ and $\bigcirc B$ meet at vertices of inscribed $n$-gons. Necessarily, $\overleftrightarrow{AB}$ is a line of symmetry for the compound polygonal figure, either passing through the polygons' vertices, or perpendicularly-bisecting the polygons' edges, or both. In any case, radial segments to the vertices of each polygon make angles with $\overleftrightarrow{AB}$ that are multiples of $\pi/n$.

Therefore, if $W$, $X$, $Y$, $Z$ are themselves vertices of these $n$-gons, then $w$, $x$, $y$, $z$ (and $\pi$!) are multiples of $\pi/n$, as are the $\angle PCQ$s. As $\pi/n = 2\pi/(2n)$ is the central angle between neighboring vertices of a $2n$-gon, we have our result.

Note: If $n$ is even, and if the polygons overlap in such a way that they have vertices on the line of symmetry $\overleftrightarrow{AB}$, then $w$, $x$, $y$, $z$ (and $\pi$!) are multiples of $2\pi/n$, so that $W$, $X$, $Y$, $Z$ are vertices of an $n$-gon about $C$.

Answer 5

This geometric problem can be expressed in purely algebraic terms, to be precise it all amounts to a certain $\mathbb Q$- linear relation between roots of unity, and this theme is a classic that has already been studied by Mann, Schoenberg, Conway and others. It follows from what we show below that $n \leq 15$.

Denote by $\Omega_A,\Omega_B,\Omega_C$ the centers of $c_A,c_B,c$ respectively, and $z_A,z_B,z_C$ the corresponding complex numbers (or "affixes" as they are called in French). Similarly, denote by $z_U,z_V,z_W,z_X,z_Y,z_Z$ the affixes of $U,V,W,X,Y,Z$. Let $\zeta$ be a primitive $n$-th root of unity.

We may assume without loss of generality that $z_A=0$. Then there are four integers $u,v,w,x\in[0,n-1]$ such that $z_U=\zeta^{u},z_V=\zeta^{v},z_W=\zeta^{w},z_X=\zeta^{x}$. For the same reason, there are two integers $y,z\in[0,n-1]$ such that $z_Y=z_B-\zeta^{y},z_Z=z_B-\zeta^{w}$.

Since $\Omega_AU\Omega_BV$, $\Omega_AX\Omega_CW$ and $\Omega_BY\Omega_CZ$ are parallelograms, we deduce $z_B=\zeta^{u}+\zeta^{v},z_C=z_W+z_X-z_A=z_Y+z_Z-z_B$.

Since $X,U,V,W$ are four distinct points on $c$, we see that $x,u,v,w$ are pairwise distinct. Similarly, $y,u,v,z$ are pairwise distinct, and $x,y,z,w$ are pairwise distinct. In the end, $x,y,z,u,v,w$ are all distinct.

Combining all those equalities, we see that

$$ \begin{array}{lcl} z_B &=& \zeta^u +\zeta^v \\ z_Y &=& \zeta^u +\zeta^v-\zeta^y \\ z_Z &=& \zeta^u +\zeta^v-\zeta^z \\ z_C &=& \zeta^x+\zeta^w = \zeta^u +\zeta^v-\zeta^y-\zeta^z \end{array}\tag{1} $$

So everything reduces to the relation $$ \zeta^x +\zeta^y+\zeta^z+\zeta^w-(\zeta^u+\zeta^v)=0 \tag{2} $$

The above is an example of what I call an $U$-relation. It is defined as a double uple $((a_1,a_2,\ldots,a_r),(\xi_1,\xi_2,\ldots,\xi_r))$ satsifying the identity $\sum_{k=1}^{r}a_k\xi_k=0$ where the $a_k$ are nonzero integers and the $\xi_k$ are distinct roots of unity. I call the integer $r$ the length of the $U$-relation. There are three natural operations on $U$-relations : permutation, rotation and multiplication by a constant. I mean by that that $((a_{\sigma(1)},a_{\sigma(2)},\ldots,a_{\sigma(r)}),\ (\xi_{\sigma(1)},\xi_{\sigma(2)},\ldots,\xi_{\sigma(r)}))$ is still an $U$-relation when $\sigma$ is a permutation of the integers between $1$ and $r$, $((a_1,a_2,\ldots,a_r),(\alpha\xi_1,\alpha\xi_2,\ldots,\alpha\xi_r))$ is still an $U$-relation when $\alpha$ is a root of unity, and $((ka_1,ka_2,\ldots,ka_r),(\xi_1,\xi_2,\ldots,\xi_r))$ is still an $U$-relation when $k\in{\mathbb Z},k\neq 0$. The regular $U$-relation in length $r$ is the $U$-relation $((1,1,\ldots,1),(1,\eta,\eta^2,\ldots,\eta^{r-1}))$ where $\eta$ is a primitive $r$-th root of unity. An $U$-relation $((a_1,a_2,\ldots,a_r),(\xi_1,\xi_2,\ldots,\xi_r))$ is said to be reducible if there is a partition $I\cup J$ of $[1,r]$ into two non-empty parts such that $\sum_{k\in I}a_k\xi_k=\sum_{k\in J}a_k\xi_k=0$. It is easy to see that a regular $U$-relation is irreducible iff its length is prime.

Theorem For any $k$, up to permutation, rotation and multiplication by a constant there are only finitely many irreducible $U$-relations of length $k$. In length $\leq 7$, the only non-regular irreducible $U$-relations are

$$ ((\epsilon_1,\epsilon_2,\epsilon_3,\epsilon_4,\epsilon_5,\epsilon_6), (-\epsilon_1\alpha,-\epsilon_2\alpha^2,\epsilon_3\beta,\epsilon_4\beta^2,\epsilon_5\beta^3,\epsilon_6\beta^4)), \tag{3} $$

where all the $\epsilon_k(1\leq k\leq 6)$ are $\pm 1$, $\alpha$ is a primitive third root of unity and $\beta$ is a primitive fifth root of unity.

Proof of theorem : see Henry B. Mann, "On linear relations between roots of unity", Mathematika 12(1965), pp.107-117.

Corollary. If we denote by $(t_1,t_2,t_3,t_4,t_5,t_6)$, the second part of (3), up to permutation and rotation there are exactly $\binom{6}{2} \times \frac{4!}{8}=15\times6=90$ solutions to (2) (with $x,y,z,u,v,w$ pairwise distinct), all of which come from (3) : they can be described by $$ \lbrace \zeta^u,\zeta^v \rbrace= \lbrace -t_i,-t_j \rbrace, \lbrace \zeta^x,\zeta^y,\zeta^z,\zeta^w \rbrace= \bigg\lbrace t_k \ \bigg| \ k\neq i, k\neq j \bigg\rbrace, \ \ 1\leq i \lt j \leq 6 \tag{4} $$

Proof of corollary By theorem, all irreducible $U$-relations of length $<6$ are regular, and so have all their coefficients of the same sign. So if (2) were not an irreducible relation, it would necessarily follows that $\zeta^u+\zeta^v=0$, so $U$ and $V$ are diametrically opposed, hence $c_B=c$ which is impossible. So (2) must be irreducible. Since it has coefficients of differents signs, it does not come from the regular $U$-relation in length $6$. So it must come from (3), which yields (4).

To count the solutions, note that there are $\binom{6}{2}$ possible values for $\lbrace i,j\rbrace$ in (4), and also that in counting the possibilities for $(\zeta^x,\zeta^y,\zeta^z,\zeta^w)$, we obtain repetitions by interchanging $x$ and $w$, by interchanging $y$ and $z$, or by interchanging $\lbrace x,w\rbrace$ and $\lbrace y,z\rbrace$. The subgroup of ${\mathfrak S}(x,y,z,w)$ fixing a given configuration has cardinality $8$.

Answer 6

Looks like false to me...

For $n=4$, which seems to satisfy $n>3$ requirement, the $A$ and $B$ squares can not intersect at opposite vertices (because they would be the same, $A=B$), so they'll have to share one side. Then there's no $X$ or $Y$ vertex between $U$ and $V$ where $C$ octagon might cross $A$ and $B$...