Maximum principle for harmonic functions on unbounded domain

Question

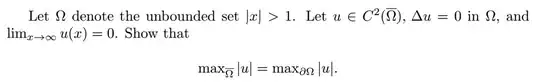
I am learning PDE by myself now. I am considering converted the problem to bounded domain to use the strong maximum principle.

My attempt:

Using the $\lim u(x)=0$, then exists $\epsilon$ and $N$, such that if $x>N$, $|u(x)|<\epsilon$. Now consider the domain $1<|x|<N$. By maximum principle, $u$ get its maximum on the boundary. if it get its maximum on $|x|=1$, then we are done. Otherwise, if $u$ get its maximum on $|x|=N$, and suppose it is $p$. Then exists $N_0>N$ such that if $x>N_0$, $|u(x)|<\epsilon/2$. So considering the domain $1<|x|<N_0$, then $p$ is a maximum in the domain, so by maximum principle, $u$ is constant. So $u$ attains its maximum on $|x|=1$. So it is proved.

I have been thinking about it for nearly 2 hours and I feel something is wrong with my proof in using the limit. I really need some help about the proof.

Can anyone help me? I will be very grateful and thanks so much!

Answer 1

The proof is correct, but the presentation could be streamlined. Here's my version.

Let $M=\max_{\partial\Omega }|u|$. We want to prove that $|u|\le M$ in $\Omega$. Fix $x_0\in\Omega$. Given $\epsilon>0$, let $R$ be such that $R>|x_0|$ and $|u(x)|< \epsilon$ when $|x|\ge R$; such $R$ exists because $u\to 0$ at infinity.

Applying the maximum principle to $u$ (and to $-u$) on $\{x:1<|x|<R\}$, conclude that $|u(x_0)|\le \max(M,\epsilon)\le M+\epsilon$. Since $\epsilon>0$ could be arbitrarily small, $|u(x_0)|\le M$. Done.