19

Why are huge binary nubers about $3.3218$ times longer than their decimal counterpart?

I thought about this when I was writing this Python code:

huge_number = 21**31**3 # ** is the power operator
print((len(bin(huge_number)) - 2) / len(str(huge_number)))
# -2 is technical stuff ignore it

No matter what the $\texttt{huge_number}$ is (it has to be huge, this does NOT work for small numbers), you will get $3.3218$. Why?

Travis Willse
  • 108,056
user3105485
  • 698
  • 43
    Hint: $10=2^{3.321928\ldots}$ – Winther Sep 18 '14 at 12:30
  • 8
    Because $\log_2(10)=3.32\ldots$. As a check on this, try converting to hex instead of decimal and examine the length-ratio. – Semiclassical Sep 18 '14 at 12:34
  • 9
    Do you see why huge binary numbers are exactly four times larger than the corresponding number in hexadecimal and exactly three times larger than the corresponding number in octal? Ten is between 8 and 16 so it should be unsurprising that 3.3218 is between 3 and 4. – Eric Lippert Sep 18 '14 at 16:13
  • 1
    @EricLippert: It's only exact for hex if you take the binary number to come in chunks of 4 bits. Otherwise you have counterexamples like $21=(10101)2=(15){16}$. (Similarly for octal.) – Semiclassical Sep 18 '14 at 17:01
  • 3
    21 is not huge. – user3105485 Sep 18 '14 at 17:02
  • 3
    @user3105485: doesn't matter, 21 times any power of 16 has the same property: in base 2 it starts with a 1 and the remaining digits come in groups of 4. So the number of digits can't be exactly 4 times any integer, although it's close to 4 times the number of hex digits. Just pick a power of 16 that you consider huge. – Steve Jessop Sep 18 '14 at 17:15
  • 1
    @Steve Jessop you are right, for example, 2116500 in hex is 3.99 times longer than in binary BUT not exactly* 4 times longer. – user3105485 Sep 18 '14 at 17:21
  • The length of a number in hex will be one-fourth the length of that number in binary, rounded up. So (length of n in binary)/(length of n in hex) is exactly 4 when the length in binary is a multiple of 4, or just a bit smaller otherwise. – Michael Lugo Feb 14 '24 at 14:36

4 Answers4

37

The number of digits of the representation of a positive integer $n$ in base $k$ is $$\ell_k(n) := \lfloor \log_k n \rfloor + 1,$$ and so the ratio of the length of a binary representation of a number to its decimal length is $$\frac{\ell_2(n)}{\ell_{10}(n)} = \frac{\lfloor \log_2 n \rfloor + 1}{\lfloor \log_{10} n \rfloor + 1}.$$

For large $n$, the constant terms in the numerator and denominator don't affect the ratio much, and neither do the differences between the values $\log_k n$ and their respective floors (which are always in $[0, 1)$), so (for large $n$) the ratio satisfies

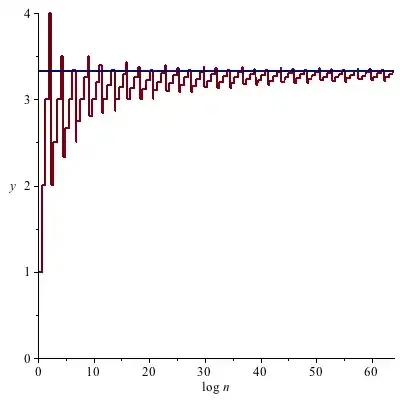
$$\color{#df0000}{\boxed{\frac{\ell_2(n)}{\ell_{10}(n)} \approx \frac{\log_2 n}{\log_{10} n} = \log_2 10 = 3.32192\ldots}}.$$

A little more precisely, the definition of floor gives that $\log_k n \leq \lfloor \log_k n \rfloor + 1 \leq \log_k n + 1$, and so $$ \frac{\log_2 n}{\log_{10} n + 1} \leq \frac{\ell_2(n)}{\ell_{10}(n)} \leq \frac{\log_2 n + 1}{\log_{10} n} . $$ Using some straightforward algebra we can rewrite this as $$ \left(1 - \frac{1}{\log_{10} n + 1}\right) \log_2 10 \leq \frac{\ell_2(n)}{\ell_{10}(n)} \leq \left(1 + \frac{1}{\log_2 n} \right) \log_2 10 .$$ As $n \to +\infty$, both of the quantities in parentheses approach $1$, so the Squeeze Theorem lets us formalize your observation as the assertion $$\lim_{n \to \infty} \frac{\ell_2(n)}{\ell_{10}(n)} = \log_2 10 .$$

Plot of $\color{#7f0000}{\ell_2(n) / \ell_{10}(n)}$ for $1 \leq n < e^{2^6}$:

enter image description here

Travis Willse
  • 108,056
  • 10
    Another way to look at it is that much like each hexadecimal digit is equivalent to 4 binary digits, and each octal digit is equivalent to 3 binary digits, each decimal digit is equivalent to about 3.3219 binary digits. – cjm Sep 18 '14 at 16:07
8

The number of digits is approximately(never off by more than 1) equal to the log in that base($\log_{10}(x)\approx$ the number of digits of x in base 10). Because of log math, you get:

$$\frac{\log_{10}(x)}{\log_2(x)}\approx 3.32193$$

Asimov
  • 3,042
  • 1
    @Semiclassical And I used approx equal signs. I fixed the part where I used the word equal. – Asimov Sep 18 '14 at 12:41
2

The fact that $$ 2^{10} = 1024 \approx 1000 = 10^3 $$ tells you that every ten binary digits need just over three decimal digits. Your question asks about exactly how many more than three (3.32...). The other answers (using logarithms, all good) identify the source of that number.

Ethan Bolker
  • 103,433
  • 1
    Slight correction: if every 10 binary digits need just over three decimal digits, then every decimal digit needs just under 10/3 binary digits, and that's where the $3.32\ldots$ comes from. – Michael Lugo Feb 14 '24 at 14:33
2

An interesting, if inefficient way to calculate logs:

import string
import math
import matplotlib.pyplot as plt

huge_number = 21**31**3
b10len = len(str(huge_number))

NUMERALS = string.digits + string.lowercase
def baseN(num, b):
    digits = []
    while num:
        digits.append(NUMERALS[num % b])
        num = num // b
    return ''.join(reversed(digits))

bases = range(2, 30)
lengths = [len(baseN(huge_number, b)) for b in bases]

f, axs = plt.subplots(ncols=2)
axs[0].plot(bases, [b10len/l for l in lengths])
axs[1].plot(bases, [math.log10(x) for x in bases])

plt.show()

enter image description here

Nick T
  • 1,803