I remember reading in a section in plato.stanford.edu that the interval $(-∞, t)$ is topologically isomorphic to the interval $(0, t)$. I am not that good with topology, so could someone show me the proof, if this is true?
Asked
Active
Viewed 287 times
2
-
1You need to establish a homeomorphism, i.e., find a continuous invertible map from $(0,t)$ to $(-\infty, t)$ with continuous inverse. Note that the $\tan(x)$ maps $(-\pi/2,\pi/2)$ to $(-\infty,\infty)$. Try modifying this function by scaling, shifting, and specifying its domain. – snar Sep 16 '14 at 00:36
3 Answers
4
A picture homeomorphism, updated with animation
Quang Hoang
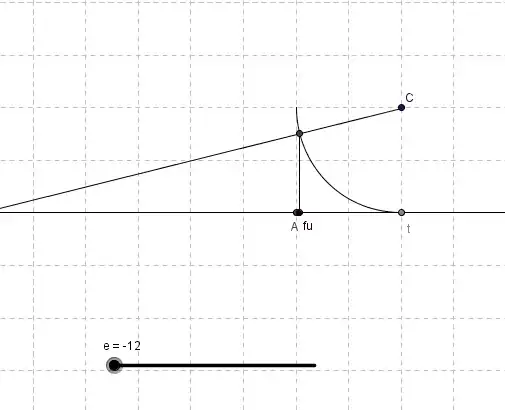
- 16,174
-
-
-
I think so. A homeomorphism, if I'm correct, is a function that is bijective, continuos and also has a continuos inverse. It is bijective, since every u value makes exactly one fu (Im taking that as f(u) ) value, which corresponds to one point on the interval (0,t). You used e, so I hope I'm correct in assuming that's exp(x). If that's the case, then it is continuous as is its inverse. – Julian Jefko Sep 16 '14 at 02:55
-
Since you asked a specific function, I change the picture. It relates to the $\tan$ function. – Quang Hoang Sep 16 '14 at 03:09
-
2
If $t>0$, then you can try the function $\phi:(-\infty,t)\to(0,t)$, defined as $$\phi(x)\equiv t\exp(x-t)\quad\forall x\in(-\infty,t).$$
Show that
- $\phi$ maps to $(0,t)$, indeed;
- $\phi$ is bijective (hint: it's strictly increasing);
- $\phi$ is continuous;
- the inverse function $\phi^{-1}:(0,t)\to(-\infty,t)$ exists and is continuous.
You will then have established that $\phi$ is a homeomorphism (“topological isomorphism,” if you will) between $(-\infty,t)$ and $(0,t)$.
triple_sec
- 23,935
-
1Why is ln(x) preferred to 1/x to send 0 to $∞$? Is it because you only need to define the function 1 way (with the knowledge that it is invertible) and that exp is continuous without exception, making the proof easier. – Richard Sep 16 '14 at 01:22
-
1I have no general preference, just thought about the exponential function first. A suitably translated and dilated reciprocal function would work perfectly fine as well. – triple_sec Sep 16 '14 at 01:42
0
I'm don't know topology, but I'm guessing that continuous real open intervals are homeomorphic if they are transformed by continuous, invertible functions over the domain [and that the inverse is continuous - thanks triple sec]. Is that right?
Some ideas here:
Homeomorphism of the real line-Topology
Here is my guess:
(0,t) f(x) = x/t => (0,1)
(0,1) f(x) = 1/x => ($∞$, 1) (1/x is continuous over that domain)
($∞$, 1) f(x) = -x => ($-∞$, -1)
($-∞$, 1) f(x) = x + t + 1 => ($-∞$, t)
