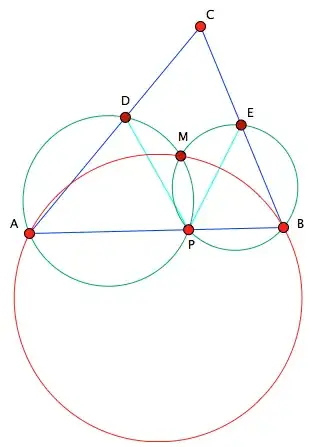
Consider an acute triangle $ABC$ and non-constant(*) point $P$ on $AB$. Take then points $D$ and $E$ on $AC$ and $BC$ respectively such that $\angle DPA=\angle EPB=\angle ACB$. Let $M$ be the intersection point, other than $P$, of the circumcircles of $\triangle APD$ and $\triangle BPE$. Find the locus of $M$
(*)I mean that P is moving on AB