derivative of $x\cdot|\sin x|$

Question

I have the function $f(x)=x|\sin x|$, and I need to see in which points the function has derivatives. I tried to solve it by using the definition of limit but it's complicated. It's pretty obvious that the function has no derivatives where $|\sin x|=0$, but I don't know how to show it. I thought maybe calculate the derivative of $f(x)$ but I didn't learn how to calculate the derivative of $|\sin x|$. How can I solve it withut knowing the derivative of $|\sin x|$? or better question how to calculate the derivative of $|\sin x|$?

edited:I didn't learn the derivative of $|f(x)|$.

Answer 1

At points where $|\sin x| = 0$, namely at integer multiples of $\pi$, the left and right-hand limits of the difference quotient of $|\sin x|$ differ, so its derivative there is undefined.

On each interval $(k, k + \pi)$, we have either $|\sin x| = \sin x$ or $|\sin x| = -\sin x$ (according to whether $k$ is even or odd respectively), and since the value of the derivative of a function at a point depends only on the value of the function at nearby points, the derivative of $|\sin x|$ on those intervals is given respectively by $\tfrac{d}{dx}(\sin x) = \cos x$ or $\tfrac{d}{dx}(-\sin x) = -\cos x$.

(There's another small technical issue here: Even though $|\sin x|$ is not differentiable at $x = 0$, $x |\sin x|$ is. In short, the factor of $x$ forces the difference quotient at $0$ to tend to $0$, so the derivative of that function at $0$ is $0$.)

Edit:

Remark It's not as important as the conceptual picture, but some people prefer explicit formulas, and here we can write

$\frac{d}{dx}|\sin x| = (-1)^{\left\lfloor \tfrac{x}{\pi} \right\rfloor} \cos(x), \qquad x \not\in \pi \mathbb{Z}$.

Answer 2

I'm going to make this as simple as I can. So, ofcourse, I'll be assuming $x\in \mathbb R$

You're first question is for what values of $x$ is the function differentiable.

There are nice algebraic ways to find it but why waste time in an explicit proof if all one needs is to convince one's peers that one's logic is right.

Let's just observe the differentiability of $f(x) = x\cdot |\sin x|$ through it's graph. But oh, wait, you must not know how to plot it's graph. So, let's take baby steps to get find it.

Take what we know. The standard graph of $y = \sin x$

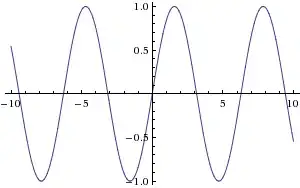
Note that the roots (ie, $\sin x = 0$) are $x = n\pi,\quad n\in\mathbb Z$

Now, let's graph y = $|\sin x|$ . How? There's a method to get $|f(x)|$ from $f(x)$ and it goes something like this:

Step 1: Make $y = 0$ a mirror which reflect all $y<0$ into the plane $y>0$
Step 2: Eliminate the portion of the graph which lies in $y < 0$
Step 3: Be amazed that by executing the above two steps precisely, you got the right graph.

^{Learn why this works}

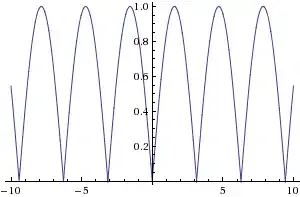
Now we have to multiply this with $x$. There's no real method for this, it only takes a slight bit of thinking and understanding of what multiplication does to a graph.

Usually when we multiply a function with a constant, say $c$.

• The graph diminishes for $c\in(0,1)$
• Enlarges for $c>1$
• Turns upside down for $c<0$ and follows the above two observations once again.

Since we're multiplying by a variable and not a pure scalar, the graph is distorted such that all the above can be seen at once and in increasing degree with increase in the magnitude of $x$.

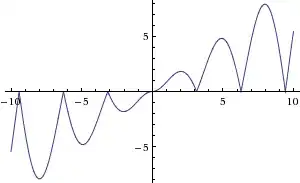
Now, it is obvious that the roots of this graph are the same as that of $\sin x$ and you know we can't differentiate a function at sharp points. (Why?)

Notice that the sharp point at $x = 0$ has been smoothed over by the inversion in the graph for $x<0$. But is it differentiable here at $x=0$?

To prove that it's differentiable at this point,

$$f'(0) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} , \quad \text{ where } x =0\\ = \lim_{h \to 0} \frac{\sin (0+h) - \sin 0}{h}\\ = \lim_{h \to 0} \frac{\sin h}{h} = 1 $$ (Why?)

$\therefore $ Derivative exists @ $x = 0$ $\implies$ Differentiable @ $x = 0$

So, we can now safely say that we can differentiate $f(x) = x\cdot|\sin x|\quad \forall \space x\in\mathbb R - \{n\pi\}, \quad n\in\mathbb Z-\{0\}$

Or more easily in words, $f(x) = x|\sin x|$ is differentiable at $x \neq n\pi ,\quad n \neq 0$

---

The following is how I would differentiate the function: $$ \frac{d}{dx} x\cdot|\sin x|\\ = \frac{d}{dx} x\cdot\sqrt{\sin^2 x} \quad ,\quad \{\because\space|x| = \sqrt{x^2}\} \\ = x\frac{d}{dx}\sqrt{\sin^2 x} + |\sin x|\frac{dx}{dx} \quad ,\quad \{\because\space (uv)' = uv' + u'v\}\\ = x\cdot\frac{1}{2\sqrt{\sin^2x}}\cdot (2\sin x)\cdot (\cos x) + |\sin x| \quad , \quad \{\because\text{Chain Rule }\}\\ =\frac{x\cdot\sin 2x}{2|\sin x|} + |\sin x|$$

This isn't totally simplified but hopefully this is helpful.

Now, to further clarify on the derivitive of $|x|$: $$\frac{d}{dx} |x| = \frac{d}{dx} \sqrt{x^2} = \frac{1}{2}(x^2)^{\frac{1}{2} - 1} \cdot 2x = \frac{2x\cdot (x^2)^{-\frac{1}{2}}}{2} =\frac{1}{2\sqrt{x^2}} = \frac{x}{|x|} \equiv \frac{|x|}{x} = \text{sgn}(x)$$

Here is more information on $\text{sgn}(x)$ and a better more explicit way of finding the derivative of the absolute value

Exercise: Can you try to get the derivative of $x|\sin x|$ with the sign-function included?

Answer 3

Let $y = x|\sin x|.$
Then $y^2 = x^2 \sin^2 x$.
So \begin{align} 2 y y' &= 2x \sin^2 x + 2x^2 \sin x \cos x\\ y' &= \frac{x \sin^2 x + x^2 \sin x \cos x}{x |\sin x|}\\ y' &= |\sin x| + x \cos x \frac{\sin x}{|\sin x|} \end{align}

When $x$ is close to, but not equal to, $0$,
$y' = |\sin x| + |x| \cos x$
It is reasonable then that
$y'|_{x=0} = 0$

Answer 4

If $\sin x_0> 0$, then $\sin x> 0$ for $x$ in a neighbourhood of $x_0$, hence $f(x)=x\sin x$ in this neighbourhood and $f'(x_0)=\sin x_0 +x_0\cos x_0$ for such $x_0$.

Likewise, if $\sin x_0< 0$, then $\sin x< 0$ for $x$ in a neighbourhood of $x_0$, hence $f(x)=-x\sin x$ in this neighbourhood and $f'(x_0)=-\sin x_0 -x_0\cos x_0$ for such $x_0$.

If $\sin x_0=0$, then $x_0$ is a multiple of $\pi$. For $x_0=0$, we find that $f'(0)=\lim_{h\to 0}\frac{h\left|\sin h\right|-0}{h} = \lim_{h\to 0}\left|\sin h\right|=0$. For $x_0=k\pi$ with integer $k\ne 0$, the limit does not exist, only the onesided limits exist: $\lim_{h\to 0^+}\frac{(k\pi+h)\left|\sin(k\pi+h)\right|-0}{h}=\lim_{h\to 0^+}\frac{(k\pi+h)\sin(k\pi+h)-0}{h}=\frac{\mathrm d}{\mathrm dx}x\sin x|_{x=k\pi}=k\pi\cos k\pi$ whereas $\lim_{h\to 0^-}\frac{(k\pi+h)\left|\sin(k\pi+h)\right|-0}{h}=\lim_{h\to 0^+}\frac{-(k\pi+h)\sin(k\pi+h)-0}{h}=\frac{\mathrm d}{\mathrm dx}x(-\sin x)|_{x=k\pi}=-k\pi\cos k\pi$, and as $\cos k\pi\ne 0$, these values differ for $k\ne 0$.

Answer 5

You know that $\sin x\ge0$ iff $2k\pi\le x\le \pi+2k\pi$ and $\sin x<0$ iff $\pi+2k\pi<x<2\pi+2k\pi$, $k\in\mathbb Z$.

Hence for $2k\pi\le x\le \pi+2k\pi$ your function is $f(x)=:f_1(x)=x\sin x$ and for the others values is $f(x)=f_2(x)=-x\sin x$.

Ok: $f_1'(x)=\sin x+x\cos x$ and $f_2'(x)=-f_1'(x)$ where are defined.

It's clear that the only interesting points are the ones in which $\sin$ vanish, i.e. $x=k\pi$. In these points you have that $f_1'(k\pi)=(-1)^kk\pi$. Moreover in these points $f_2$ is not defined, however in order to understand what happens with the other "piece" of derivative, you can pass to the limit and see that $\lim_{x\to k\pi}f_2'(x)=(-1)^{k+1}k\pi$.

Hence the two "pieces" agree iff $k=0$. Hence you can conclude that

$$ f'(x) = \left\{ \begin{array}{rl} f_1'(x) & \mbox{if }\;\;\; 2k\pi< x\le \pi+2k\pi \\ f_2'(x) & \mbox{otherwise } \\ 0 & \mbox{if}\;\;\; x=0 \end{array} \right. $$

I.e. the function $f$ is derivable in the whole $\mathbb R$ except the point $k\pi$, with $k\in\mathbb Z\setminus\{0\}$