How to obtain asymptotes of this curve?

Question

I am reading a text, where the neutral curve as a result of linear stability analysis of a delayed differential equation is given. $\delta$ and $\alpha$ are parameters of this model. The curve is defined as

$$ \delta=\arccos\left(\frac{3\alpha-2}{\alpha}\right)\frac{1}{\sigma_i(\alpha)},$$

where

$$\sigma_i(\alpha)=\sqrt{\alpha^2-(2-3\alpha)^2}.$$

Furthermore, I know that $\delta\gt 0$ and $0\lt\alpha\leq 1$.

I do understand how these equations are derived. However, I do not understand where the the following statement comes from:

This curve asymptotes to $\alpha=1/2$ for large $\delta$ and $\alpha=1/\delta$ for $\delta$ near $1$.

I can see a approximately how the first asymptote is derived, as $\sigma_i(1/2)=0$. Then $\delta\to\infty$. However, I have no clue on how to arrive at the second asymptote. How can this be derived?

Answer 1

To say $\alpha=1/\delta$ for $\delta$ near $1$ is to say $\alpha=1/\delta$ for $\alpha$ near $1$. So we look at the limit of $\delta\left(\alpha\right)$ as $\alpha \rightarrow 1$.

To show the asymptote exists, we need to show both $\lim_{\alpha \rightarrow 1}{\delta\left(\alpha\right)} = \lim_{\alpha \rightarrow 1}{1/\alpha} = 1$ and $\lim_{\alpha \rightarrow 1}{\delta'\left(\alpha\right)} = -1$ ($-1$ being the gradient of curve $\delta = 1/\alpha$ at point $\alpha = 1$).

$\lim_{\alpha \rightarrow 1}{\delta\left(\alpha\right)} = \lim_{\alpha \rightarrow 1}{\frac{\arccos{\left(\frac{3\alpha - 2}{\alpha}\right)}}{\sqrt{\alpha^2 - \left(2 - 3\alpha\right)^2}}} $.

This is a $0/0$ limit so we use l'Hopital's rule with:

$f\left(\alpha\right) = \arccos{\left(\frac{3\alpha - 2}{\alpha}\right)}\qquad$ and $\qquad g\left(\alpha\right) = \sqrt{\alpha^2 - \left(2 - 3\alpha\right)^2}$.

Then, \begin{eqnarray*} f'\left(\alpha\right) &=& \frac{-2}{\alpha^2 \sqrt{1 - \left(\frac{3\alpha - 2}{\alpha}\right)^2}} \\ && \\ &=& \frac{-2}{\alpha \sqrt{\alpha^2 - \left(2 - 3\alpha\right)^2}} \end{eqnarray*} and \begin{eqnarray*} g'\left(\alpha\right) &=& \frac{-8\alpha + 6}{\sqrt{\alpha^2 - \left(2 - 3\alpha\right)^2}}. \end{eqnarray*}

So, \begin{eqnarray*} \lim_{\alpha \rightarrow 1}{\delta\left(\alpha\right)} &=& \lim_{\alpha \rightarrow 1}{\frac{f'\left(\alpha\right)}{g'\left(\alpha\right)}} \\ && \\ &=& \lim_{\alpha \rightarrow 1}{\frac{\frac{-2}{\alpha \sqrt{\alpha^2 - \left(2 - 3\alpha\right)^2}}}{\frac{-8\alpha + 6}{\sqrt{\alpha^2 - \left(2 - 3\alpha\right)^2}}}} \\ && \\ &=& \lim_{\alpha \rightarrow 1}{\frac{1}{4\alpha^2 - 3\alpha}} \\ && \\ &=& 1. \end{eqnarray*}

This completes the first part, and it might be enough for your purpose, but to show it is actually asymptotic, the limit of the function derivative also needs to be equal to that of the asymptote derivative.

In my calculation (involving some tedious limit evaluations), $\delta'\left(\alpha\right) \rightarrow -\frac{5}{3}$ as $\alpha\rightarrow 1$. In which case it's not asymptotic to $\delta = 1/\alpha$ in the strict sense. But the function $\delta\left(\alpha\right)$ is approaching a fixed point $\left(\alpha,\delta\right) = \left(1,1\right)$ rather than going off to infinity in some direction where asymptotic behaviour is normally seen/discussed.

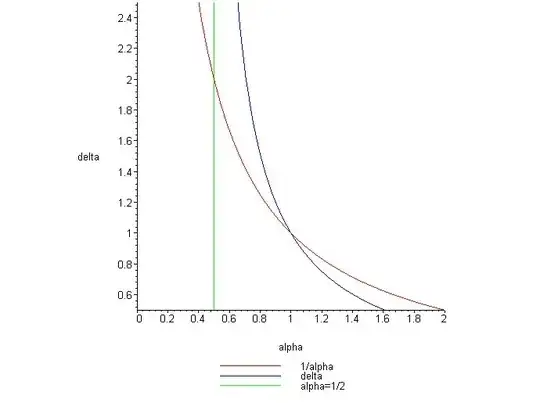
Plot from Maple of the $\delta\left(\alpha\right)$ and the two "asymptotes" mentioned. When the text says "above these two lines", you have to look at the graph sideways to get their meaning. :-) But it is true (within the range $0 \leq \alpha \leq 1$).