6

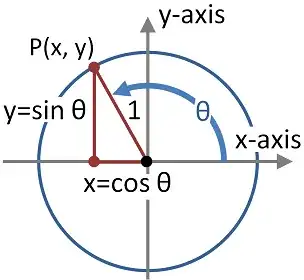
There are circular (trig) functions which determine all the points on a unit circle: enter image description here
and which relate to the area swept out by an angle subtended on the circle.
-- These functions can of course be extended to relations to ellipses as well.

There are also hyperbolic functions which determine all the points on a hyperbola:
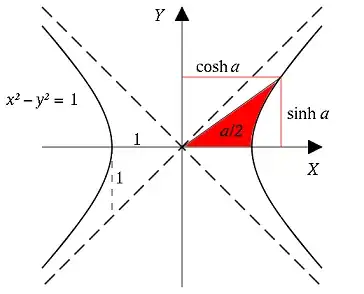
insert pic.

My question is why there are no analogs of these functions for parabolas (the other type of conic section):
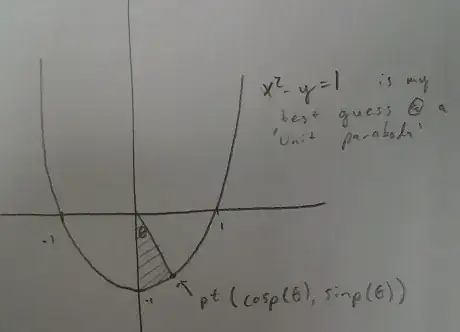
insert pic.
Here I have defined $\mathrm {sinp}(\theta)$ and $\mathrm {cosp}(\theta)$ to be the x- and y-coordinates of points on a "unit parabola".

Is there any good reason why we should have these extremely useful transcendental functions (sin, cos, sinh, cosh, etc), but we can't (or don't) define analogous functions for parabolas?

NOTE: I recommended that this post get deleted because Henning's response in Do "Parabolic Trigonometric Functions" exist? explained theoretically why a "parabolic trigonometric function" is different than the circular and hyperbolic trigonometric functions. However johannesvalks' answer to this was very interesting, as well, and probably shouldn't be deleted.

Community
  • 1
user157624
  • 113
  • It is very possible that there do exist such functions but they are not of much use so there is little focus on them. – Brad Jun 17 '14 at 15:11
  • Under sections of a parabola huh? Which parabola are you considering? The line segment $(0,0)$ to $(x,x²)$ lies generally above the parabola, so there is no "under". – Willie Wong Jun 17 '14 at 15:18
  • I don't get your picture. The analogous picture for the circle has area $A(\theta) = \frac12\theta$, if the radius is assumed to be $1$. Where does the trigonometric functions come in? – Willie Wong Jun 17 '14 at 15:22
  • The parabola is birationally equivalent to the affine line, whereas the circle and the hyperbola are not. Therefore it is natural that special transcendental functions will be required to parametrize the circle and hyperbola, while the parabola only needs polynomials. – ziggurism Jun 17 '14 at 15:41
  • From wikipedia's Birational Geometry page: "For example, the circle with equation $x^2 + y^2 − 1 = 0$ is a rational curve, because the formulas $x= \frac {2t} {1+t^2}$ & $y= \frac {1-t^2} {1+t^2}$ define a birational map from the affine line to the circle." So unless I'm not understanding (very probable), there does seem to be a birational mapping from the circle to the affine line. – user157624 Jun 17 '14 at 16:53

2 Answers2

1

Such functions do exist! They're called cubic polynomials:

$$\int_a^b x^2 dx=\frac13(b^3-a^3)$$

David H
  • 32,536
  • Sorry, I didn't phrase the area I meant well enough. I'll edit with a picture... Or I would except that my computer is screwing up. Hold on. – user157624 Jun 17 '14 at 15:06
  • @user157624 I see. Perhaps you're looking for something more like this? http://mathworld.wolfram.com/ParabolicSegment.html – David H Jun 17 '14 at 15:32
1

Note that

(1) For $\cos(\phi)$ and $\sin(\phi)$ the argument is a 'surface'.

(2) For $\cosh(\zeta)$ and $\sinh(\zeta)$ the argument is a 'surface'.

So you should look for functions where the argument is a 'surface'.

Consider $y = x^2 - c$, where $c$ is positive.

For a given $x = \xi$ we have an arc formed by:

(3a) the curve $(0,-c) \rightarrow (\xi,\xi^2-c)$

(3b) the line $(\xi,\xi^2-c) \rightarrow (0,0)$

(3c) the line $(0,0) \rightarrow (0,-c)$

The surface of this arc is given by

(4) $\displaystyle A = \int_0^\xi \left( \frac{\xi^2 - c}{\xi} x + c - x^2 \right) dx = \frac{1}{6} \xi^3 + \frac{1}{2} c \xi$

So for a point $(x,y)$ on the curve $y = x^2 - c$ we obtain

(5) $A = \frac{1}{6} x \Big( x^2 + 3c \Big)$

And what we want is

(6a) $x = x(A)$

(6b) $y = y(A)$

To find the inverse for $A = \frac{1}{6} x \Big( x^2 + 3c \Big)$, we write $\displaystyle x = \frac{c}{\zeta} - \zeta$, then we get the equation

(7) $\Big[ \zeta^3 \Big]^2 + 6 A \Big[ \zeta^3 \Big] + c^3 = 0$,

whence

(8) $ \zeta^3 = \sqrt{9A^2 + c^3} - 3A $,

therefore

(9a) $\displaystyle x(A) = \frac{c}{\sqrt[3]{\sqrt{9A^2 + c^3} - 3A}} - \sqrt[3]{\sqrt{9A^2 + c^3} - 3A}$

The 'parabolic' functions are given by

(10a) $\displaystyle x(A) = \frac{c}{\sqrt[3]{\sqrt{9A^2 + c^3} - 3A}} - \sqrt[3]{\sqrt{9A^2 + c^3} - 3A}$,

(10b) $\displaystyle y(A) = \frac{c^2}{\sqrt[3]{\sqrt{9A^2 + c^3} - 3A}^2} + \sqrt[3]{\sqrt{9A^2 + c^3} - 3A}^2 - 3 c$,

but they can be expressed using radicals, as is not the case for goniometric and hyperbolic functions.

The case $c=1$ gives

(11a) $\displaystyle x(A) = \frac{1}{\sqrt[3]{\sqrt{9A^2 + 1} - 3A}} - \sqrt[3]{\sqrt{9A^2 + 1} - 3A}$,

(11b) $\displaystyle y(A) = \frac{1}{\sqrt[3]{\sqrt{9A^2 + 1} - 3A}^2} + \sqrt[3]{\sqrt{9A^2 + 1} - 3A}^2 - 3$.

johannesvalks
  • 6,587