How to find camera position and rotation from a 4x4 matrix?

Question

To find the intrinsic and extrinsic parameters, I calibrated it and the software gave me the extrinsic parameters as a 4 x 4 matrix. This seems to be a 4x4 homogeneous transformation matrix.

The values are as follows:

$$ \left( \begin{array} 0.211 & -.306 & -.928 & .789 \\ .662 & .742 & -.0947 & .147 \\ .718 & -.595 & .360 & 3.26 \\ 0 & 0 &0 & 1 \\ \end{array} \right) $$ I also have the intrinsic parameters of the camera like focal length, principal point, skew, distortion coefficients, etc.

How do I extract the camera position and rotation in world coordinates using this matrix?

EDIT:

cam image

On the left, I have shown a cam and its viewing a 3d object, and I take a photo of this 3D object from the cam. The right is what I want. I want to get the world position/rotation of the cam and the world position/rotation and actual size of the image in 3d space.

The top 3x3 block is the rotation, and the right column is the translation. I can't say more without information about what this matrix is suppose to be: the map from some reference pose of the camera to its current position (and what is that reference position?) The inverse of this map? — user7530, Nov 16 '11 at 06:59
From http://en.wikipedia.org/wiki/Camera_resectioning I found that this is an matrix for extrinsic parameters of the camera. It consists of R and T. It says that the camera position can be found by using C = -R' . T Don't know if thats the way to go? — Kevin Boyd, Nov 18 '11 at 05:58
Think of the right camera as a projector: it shines an image onto whatever surface it is pointing at. There is no "actual size" of the image it is projecting: move the screen closer and you get a smaller image; farther and you get a larger one. You can measure the distance from the left camera to the left box, and the put the screen at the same distance on the right; but to do this, you need to know the position of the left camera (see my answer below) and the position of the box. The position of the box in world coordinates is not something you can infer from your matrix, or the image. — user7530, Nov 21 '11 at 11:35
Here's a question that might clarify what you want: suppose, instead of the box on the left, there's a person in the foreground and the Eiffel Tower in the background, so that both the person and the tower appear the same height in the 2D picture captured by the left camera. What do you expect to see on the right? — user7530, Nov 21 '11 at 11:44
@user7530 Hello user! What you say seems make some sense. Since I have other details like Focal length, principal point and also exif data save in the image along with the camera matrix isn't this sufficient information for getting the details. I'm the dumb guy here so I don't know what is possible and what is not. I had posted a question here and as per the images those guys seem to be get something close to what I want. — Kevin Boyd, Nov 23 '11 at 11:13
Unfortunately these intrinsic parameters still aren't enough to tell you the position of the box. (Notice that in the SO question and answer, the position of the corners of the plane in world coordinates is exactly known.) — user7530, Nov 23 '11 at 11:35
@user7530 any idea of a process or algorithm that would get the position of the box? What additional steps would I have to do to gather the box position data? — Kevin Boyd, Nov 23 '11 at 15:58
A nice explanation here as well:
http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MARBLE/high/pose/express.htm — Mircea, Feb 12 '19 at 13:25

score 31 · Accepted Answer · answered Nov 19 '11 at 08:07

31

Assuming your matrix is an extrinsic parameter matrix of the kind described in the Wikipedia article, it is a mapping from world coordinates to camera coordinates. So, to find the position $C$ of the camera, we solve

$$\begin{align*}0 &= RC + T\\ C &= -R^T T \approx (-2.604, 2.072, -0.427).\end{align*}$$

The orientation of the camera is given simply by $R^T.$ So if the "in" axis is the z-axis, for instance, then the vector pointing in the direction the camera is pointing is

$$R^T \left[\begin{array}{c}0\\0\\1\end{array}\right] = (0.718, -0.595, 0.36).$$

answered Nov 19 '11 at 08:07

user7530

50,625

Excellent answer, user7530, I didn't understand the "in" axis part. Another question once I draw the camera position in 3D space I would also like to draw the actual image and its location and angle in 3D is that possible using the matrix? – Kevin Boyd Nov 20 '11 at 08:18
There are three axes in the camera's coordinate system: left-right, up-down, and into the picture. I am assuming that $z$ is the "into the picture" axis (i.e., that the camera is looking down the z-axis.)
I'm not sure what you mean. You want to take what the camera sees, and project this 2D image onto a 2D "canvas" in the 3D scene?

user7530

Nov 20 '11 at 08:29

I've edited my question. I hope the image explains it better now. – Kevin Boyd Nov 21 '11 at 11:13

Thank you very much for your response. What do you mean with "in" axes? I'm using a right handed reference XZY where Z is the Up direction and I'm not able to get the orientation to work correctly by using R_transpose .. am I doing something worng? – rkachach Oct 16 '18 at 12:37

could you please also look at this – user0193 Jun 10 '21 at 15:29

John Calsbeek · Answer 2 · 2011-11-22T07:53:20.843

6

I am not familiar enough with this domain to know what the conventions are, but I can provide some general context.

A $4 \times 4$ homogeneous camera matrix transforms coordinates from world space to camera space. Apparently, this matrix does not include a perspective projection, so we're effectively talking about an affine transformation. The matrix itself can tell you where the camera is in world space and in what direction it's pointing, but it can't tell you anything else—you need other parameters of the camera for that.

Because we're just talking about a transformation here, we need conventions to tell us about the camera. The conventions that I'm used to are that in camera space, the camera is situated at the origin, and has axes that look like this:

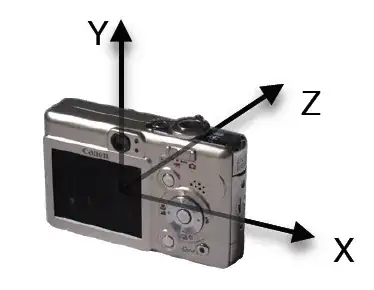
camera axes

In other words, the camera is looking along the positive Z axis, and the Y axis is up. In this system, you can transform the vector $\left[0, 0, 1\right]$ by the transformation's inverse to get the camera's viewing vector in world space, and the point $\left[0, 0, 0\right]$ to get the camera's position in world space.

The general form of this is that the camera's position is $M^{-1} \, \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \right]$ and the camera's viewing vector is $M^{-1} \, \left[\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array} \right]$, but if you have a matrix that looks like

$$\left[\begin{array}{cccc}\phantom{M}&&&\ \\ & R & & T \\ &&& \\ 0 & 0 & 0 & 1 \end{array} \right]$$

where $R$ is a $3 \times 3$ matrix and $T$ is a vector, then the camera position is just $-R^T T$ and the camera viewing direction is $R^T \, \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right]$.

This tells you about as much as you can possibly get from the matrix. Everything else depends on the other properties of the camera.

edited Nov 22 '11 at 07:53

answered Nov 21 '11 at 11:48

John Calsbeek

269

1

+1 For the effort! even though I don't understand the math ;) – Kevin Boyd Nov 22 '11 at 05:38
Interesting point you make regarding the affine transformation, I wasn't aware that we don't have perspective projection data, I always thought that the matrix gave us the projected information. Isn't affine transformation some kind of parallel projection. – Kevin Boyd Nov 22 '11 at 05:42
"Affine transformation" means that the transformation can do anything a linear transformation can do (rotate, scale, shear) plus also translate.
The $4 \times 4$ homogeneous matrix is capable of doing perspective projections, but this one doesn't—as would be expected by convention for something called the "camera matrix." The remaining intrinsic parameters, in this case, would control the projection.
– John Calsbeek Nov 22 '11 at 07:44
Hi John!, you have mentioned that -R'T is the cam position and is the camera direction given by multiplication of R' and [0 0 1] where the matrix is a column vector?? – Kevin Boyd Nov 23 '11 at 11:19
That's correct. – John Calsbeek Nov 24 '11 at 23:07
John! one more question why do you negate the multiplication of R' * T to get the cam position. And why do you need to transpose the matrix R to get position and rotation. – Kevin Boyd Dec 13 '11 at 19:03
The camera position is just solving the equation that user7530 also posted.
Because R is a rotation matrix, transposing it does the same thing as taking its inverse; so you can think of it as transforming the value in reverse.
– John Calsbeek Dec 13 '11 at 19:08
Thanks, John! You helped me quite a lot. I have been sitting on a similar problem for a few days. Your solution for affine transformations with pos = -(R^T)T works fine. However when I try to use your general solution with (M^-1)(0,0,0,1), I get weird results (even though I only use affine transformation matrices for M). Is there perhaps a mistake in that formular? – Lukas Schmelzeisen Nov 25 '12 at 21:22
1

@LukasSchmelzeisen It should work, but it may not apply to your situation. If M changes from one space to another, then that expression picks off the last column of M^-1, which is the translation in the original space that reverses the translation performed by M. If M can be thought of as moving a camera to the origin, then that expression produces the position of the camera in the original space. – John Calsbeek Nov 25 '12 at 23:26
1

@LukasSchmelzeisen If you have an affine transformation matrix, then it should match the form where the upper-left 3x3 is R, a rotation matrix, and where the last column is T, at which point the expression in question should be identical to -(R^T)T. – John Calsbeek Nov 25 '12 at 23:28
Why don't you use standard right-handed system? Y should be pointing down for standard axis in right-handed system – Ginés Hidalgo Jun 03 '18 at 21:48

How to find camera position and rotation from a 4x4 matrix?

2 Answers2