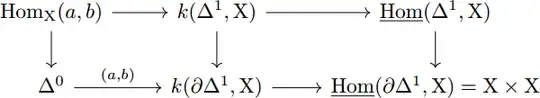11

Let $X$ be a quasi-category. (i.e. a simplicial set satisfying the weak Kan extension condition). Given two 'objects' $a,b\in X_0$ in $X$, one defines the mapping space $X(a,b)$ to be the pullback of $$ X^{\Delta^1}\to X^{\partial\Delta^1}\cong X\times X $$

Along the map $pt\to X\times X$ that takes the point to the pair $(a,b)$. It is (apparently) well known that $X(a,b)$ is always a Kan complex (provided $X$ is a quasi-category as we assumed). How does one prove this? I've seen this stated in several papers of Joyal, but without a proof and with references to some unfindable sources. I am sure this also appears somewhere in Lurie's HTT , but I got lost in all the different mapping space objects that he uses. An outline of the argument or a readable self contained reference would be very much appreciated.

Zhen Lin
  • 97,105
KotelKanim
  • 2,986

3 Answers3

6

The proof appears quite late in HTT. The simplicial set $X (a, b)$ (in Lurie's notation, $\mathrm{Hom}_X (a, b)$) is first mentioned after Remark 1.2.2.5, and the fact that it is a Kan complex appears implicitly in Corollary 4.2.1.8. A similar result appears as Corollary 4.8 in [Dugger and Spivak, Mapping spaces in quasi-categories], but they do not explicitly state that $X (a, b)$ (in their notation, $\mathrm{Hom}_X^\mathrm{cyl} (a, b)$) is a Kan complex. (They are more interested in showing that the different models of hom-spaces are weakly equivalent.)

I should probably mention that it is comparatively easy to show that $X (a, b)$ is a quasicategory. Indeed, the class of inner fibrations is well behaved with respect to exponentiation, so the projection $[\Delta^1, X] \to [\partial \Delta^1, X]$ is an inner fibration; and the class of inner fibrations is closed under pullback, so $X (a, b) \to \Delta^0$ is also an inner fibration, i.e. $X (a, b)$ is a quasicategory. In principle, it then suffices to prove that the "homotopy category" $\tau_1 (X (a, b))$ is a groupoid, but I don't see any quick way of doing this.

Zhen Lin
  • 97,105
6

As Zhen noted, $\newcommand{\Hom}{\mathrm{Hom}}\Hom_X(a,b)$ is an $\infty$-category and it suffices to show that every 1-morphism of $\Hom_X(a,b)$ is an equivalence. In particular it is sufficient to show that every $(2,0)$-horn $\Lambda^2_0 \to \Hom_X(a,b)$ can be filled. One can translate this to the condition that any morphism $$ \Lambda^2_0 \times \Delta^1 \bigsqcup_{\Lambda^2_0 \times \partial\Delta^1} \Delta^2 \times \partial\Delta^1 \longrightarrow X, $$ that maps $\Lambda^2_0 \times \{0\}$ to $a$, lifts to a morphism $\Delta^2 \times \Delta^1 \to X$. Since in particular the 1-simplex $d^2(\Delta^2) \times \{0\}$ is mapped to an equivalence of $X$, the claim follows from Proposition 2.4.1.8 of HTT. To see how that proposition is applied here, see the proof of Lemma 2.3.3.5, for example. It may be overkill here, though, the idea is just the same as the proof of the implication (1) => (2) in Proposition 2.1.2.6 (Joyal's characterization of left anodyne maps).

2

$\newcommand{\Hom}{\mathrm{Hom}}$There is another simpler argument suggested in these notes of Denis-Charles Cisinski:

For an $\infty$-category $X$, let $k(X)$ denote the maximal sub-$\infty$-groupoid of $X$. Write $\newcommand{\uHom}{\underline{\mathrm{Hom}}}k(A, X) = k(\uHom(A, X))$ for any simplicial set $A$. Then the cartesian square defining the mapping space $\Hom_X(a,b)$ factors into two cartesian squares

mapping space

The point here is the theorem:

Theorem. Let $p : X \to Y$ be a fibration of $\infty$-categories in the Joyal model structure. For all monomorphisms $u : A \hookrightarrow B$, the morphism $$ q : k(B, X) \longrightarrow k(A,X) \times_{k(A,Y)} k(B,Y) $$ is a Kan fibration.

Hence one sees that the middle vertical morphism is a Kan fibration, and therefore so is the left vertical morphism.

See page 117 in the notes referenced above for the proof of this theorem.

Martin Sleziak
  • 56,060