Consider the 6-node ring with only one bit active (000001). This is shown in the following figure as a hexagon with one circle filled.
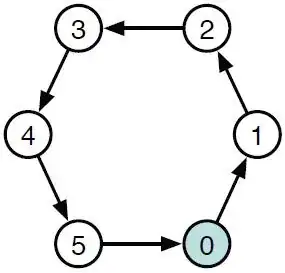
If the active bit is traveling in the counter clockwise
direction, we can represent the transitioning bit string as follows:
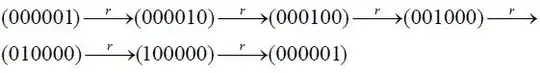
After six-rotations, r, the ring is in the same configuration as when we started. Symbolically we can
represent this as:
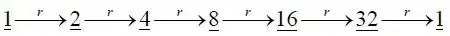,where the numbers represent the decimal equivalent of the bit string.
Also, they are
underlined to remind us that these are group symbols not numbers to be manipulated as numbers.
This string of elements interspersed with a rotation operation represents the
elements for the group and the main operation.
We represent this group by $G^6_1$ where the
superscript reminds us that the group is for six-node rings and the subscript is the lowest
decimal equivalent of the bit string in this group.
The $G^6_1$ group can now be written as $G^6_1=\{\underline{1}, \underline{2}, \underline{4}, \underline{8}, \underline{16}, \underline{32} \}. $
Thus, the full set of all the groups $G^6=\{G_1^6,G_5^6,G_9^6,G_21^6\}$ is given as:
Define the operator $\Phi_{nr}$ which transforms one group into another group in $G^6$, where the subscript on the operator represent the number of rotations when the pulse is injected. For example, in $G^6$ sensor fusion operator group transformations, consider $\Phi_2 (G_1^6)\to G_5^6$. This equation says that when the CPG circuit has one cycling through the ring and if a pulse of duration equal to the time constant of the neurons is injected at rotation 2 (subscript to operator) this will be the equivalent of initializing the ring circuit with (000101) or decimal 5. Thus, So the circuit is transformed to the $G_5^6$ group. Explicitly this would be written as $(000100) + (000001) \to (000101).$ Example 2.Consider $\Phi_{23}(G_1^6) \to G_9^6$. This means that when a pulse of two time constants are injected at rotation positions 2 and 3 into a 6-node circuit with a signal already at position 0 (always the assumed initial state), the circuit pulse pattern will transform to $G_9^6$. Explicitly this would be written as $(000001) + (000110) \to (0001001).$
Question: I've checked that $(000001) + (000110) \to (0001001)$ does not follow with the rules of binary addition. My question is how did the author established this expression? Is there any algorithm to follow? Any help is greatly appreciated.
