how to find an upper bound of the spectral radius

Question

I've given the real valued matrix $K=K_1+K_2$, with $K_1$ and $K_2$ symmentric and positiv defined. Further there are given this 3 matrices:

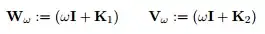
with $\omega > 0$ and

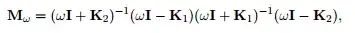
Now I tried the whole day to show this:

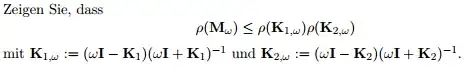
and this:

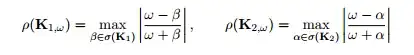
Could somebody help me ???

My idea was the following: In every bracket of the matrix $M$ there is a symmetric positiv defined matrix. Hence we know $A*B=(B*A)^t$ (here the small t means transposed). With this in mind I tried to change the order of the brackets in M and the to use the triangle inequality to get the claim, but I didn't reached it.

I would be very happy if someone has a better idea

Answer 1

Hints. Here are a few useful facts ($X,Y$ below denote complex square matrices):

1. $\rho(XY)=\rho(YX)$. This follows from a well-known fact that $XY$ and $YX$ have identical characteristic polynomials. (See also q311342.)
2. Normal (including Hermitian) matrices are unitarily diagonalisable. I think this is taught in virtually every introductory course on linear algebra.
3. When both $X,Y$ are normal, their spectral radii coincide with their induced 2-norms and hence $\rho(XY)\le\|XY\|_2\le\|X\|_2\|Y\|_2=\rho(X)\rho(Y)$.
4. For any scalars $\alpha$ and $\beta$, the matrices $\alpha I+X$ and $(\beta I+X)^{-1}$ commute (provided that the latter inverse exists). This is a consequence of Cayley-Hamilton theorem when applied to the matrix $\beta I+X$.