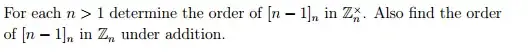
Do they mean find a general formula such that for any n we can find its order by substituting its value in the formula? If so how do we go about doing this?
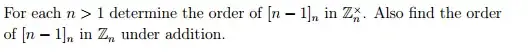
Do they mean find a general formula such that for any n we can find its order by substituting its value in the formula? If so how do we go about doing this?
The additive order of $n-1$ in $\Bbb Z_n$ is $n$. That's it's a generator for the additive group, since $(n,n-1)=1$.
Note: $$n-1=(n-1)\cdot 1\overset{\text{in multiplicative notation}}{\overbrace{=}}1^{n-1}\implies \lvert n-1\rvert =n/(n,n-1)=n.$$
Here's a proof of that formula.
I dont think they mean for any $n$ since no such formulas exist. For $n-1$, note that the order is just $2$ since $(n-1)^2 \equiv (-1)^2 \equiv 1 \pmod n$.
For addition, the order is infinity for any element in the set since we can never get back to our identity element.