10

how do I find a Lipschitz constant for $e^{-x^2}$? This is homework so I'd just like some tips on how to proceed. I've got $|e^{-x^2}-e^{-y^2}| = |(e^{-x^2+y^2} -1)||e^{-y^2}| < a$ where $a = -x^2 +y^2$.

I'm not sure how to proceed so any help will be appreciated! Thanks!

Thanks that makes sense!

user134919
  • 161
  • 3
    Can you use the mean value theorem? – Carsten S Mar 12 '14 at 12:25
  • $f(x) = e^{-x^21}$ is differentiable on the whole real line, meaning any $M$ with $M \geq f'(x)$ for all $x \in \mathbb{R}$ will work as a lipschitz constant. As Carsten Schultz already pointed out, you can prove this via the mean value theorem. Write $f(y)$ as $f(x) + \int_{x}^{y} f'(z) dz$, and use $f'(z) \leq M$ plus the mean value theorem to bound the integral. – fgp Mar 12 '14 at 13:25
  • @user134919 answer edited – Bman72 Mar 12 '14 at 21:19

1 Answers1

17

I would solve it like this: you have that $f(x) = e^{-x^2}$. This is the graph of your function:

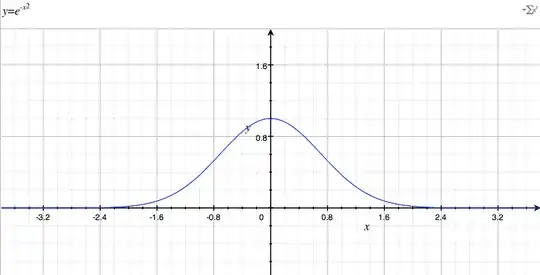
As you can see there are two points around $-0.8$ and $0.8$ where the slope is the highest one. The definition of Lipschitz continuous says:

A function $f: \mathbb{R} \to \mathbb{R}$ is Lipschitz continuous if there exists some constant L such that:

$$\vert f(x) - f(y)\vert \le L |x-y|$$

Since your $f$ is differentiable, you can use the mean value theorem, $$ \frac{f(x) - f(y)}{x-y} \leq f'(z) \quad\text{for all $x < z < y$,} $$ and deduce that it is sufficient to find a bound $L$ with $|f'(z)| \leq L$ for all $z \in \mathbb{R}$.

Now from your graph the important thing that you have to understand is if the slope in the points around $-0.8$ and $0.8$ is lower or bigger than $1$ (because there the slope assumes obviously the biggest values). If it's lower than $1$ you can choose $L=1$ and you have $|f(x) - f(y) \le |x-y|$ because the slope of the function is lower than $1$ and this means that the distance between the images of $f(x)$ is lower than the distance between the arguments in every point $x,y \in \mathbb{R}$.

So let's look after the maximal value of the slope of your function $f(x)$ to do that we calculate the derivative of $f(x)$ given by:

$$f'(x) = -2x e^{-x^2}$$

This is the graf of the function $f'(x)$:

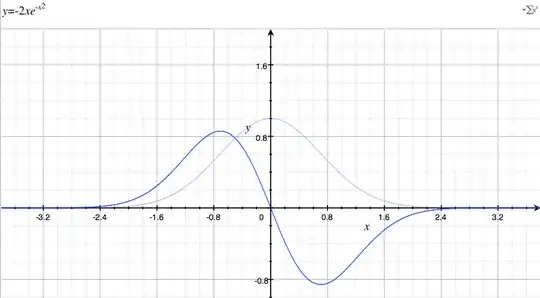
You see that as we said she assumes the maximal values around the points $-0.8$ and $0.8$ to get the exact value we have to derivate once again $f'(x)$ and look for which point the functions is equal to $0$:

$$f''(x) = -2e^{-x^2} + 4x^2e^{-x^2} = e^{-x^2} * (-2 + 4x^2)$$

Now

$$f''(x) = 0 \iff (4x^2 -2) =0$$

since $e^{-x^2}$ will never be $0$

$$\iff x = +\frac{1}{\sqrt(2)} \lor x = -\frac{1}{\sqrt(2)}$$

Now you notice that $f'(\frac{1}{\sqrt(2)}) = -\sqrt{\frac{2}{e}} \gt -1$ and $f'(-\frac{1}{\sqrt(2)}) = \sqrt{\frac{2}{e}} \lt 1$

Now you are allowed to take $L = 1$ and you have your Lipschitz continuity :-)

Ѕᴀᴀᴅ
  • 35,369
Bman72
  • 2,863
  • 1
  • 17
  • 30
  • Hm, this assumes that one already knows that for differentiable functions, any bound on the derivative works as a lipschitz constant. That's not immediately obvious, though - the derivate takes the limit of the differential quotient, yet for a lipschitz constant you need a bound on the differential quotient itself. But it's not generally true that $\lim_{n\to\infty} a_n \leq a$ implies $a_n \leq a$ for all $n$... – fgp Mar 12 '14 at 13:31
  • Also, you don't usually require your lipschitz constant to be exact, so finding the actual maximum of $f'$ is a bit of overkill. It suffices to find some $M$ such that $f'(x) \leq M$ for all $x \in \mathbb{R}$. – fgp Mar 12 '14 at 13:33
  • @fgp you are right, you don't need a precise constant $L$ but my $L=1$ was random, you could have taken $L=2$ it is the same, the important thing is that there exists one. Moreover the derivative of a functions is the slope of the functions i.e: $\frac{f(x)-f(y)}{x-y}$ now if she is $\lt 1$ $\forall x,y$ wouldn't follow automatically that $f(x) - f(y) \lt 1* (x-y)$? maybe I'm wrong ;-) or what did you exactly mean? – Bman72 Mar 12 '14 at 13:54
  • It doesn't really "follow automatically" (at least not for me). $f'(x) \leq 1$ means $\lim_{x\to y} \frac{f(x)-f(y)}{x-y} \leq 1$, but the lipschitz condition requires $\frac{f(x)-f(y)}{x-y} \leq 1$ for all $x,y$. That's, at least initially, a stronger condition! It's entirely conceivable that some differential quotient could be $> 1$, yet the limit for $x \to y$ could always end up $\leq 1$. Thus, you need to prove that this, indeed, is impossible. – fgp Mar 12 '14 at 14:16
  • Your are again right, but since the function $f(x) = e^{-x^2}$ is continuously differentiable this means that the quotient is defined for all x and y and since the quotient takes the maximal values at ${1 \over \sqrt(2)}$ and $-{1 \over \sqrt(2)}$ and there the derivative of $f$ is lower than $1$ than this would be enough, isn't it? – Bman72 Mar 12 '14 at 14:18
  • But you didn't show that the quotient takes the maximum value at $\frac{1}{\sqrt{2}}$! That's not even a well-defined statement, since the quotient as two parameters - $x$ and $y$. What you showed is that the limit of the quotient for $x \to y$ has a maximum at $y=\frac{1}{\sqrt{2}}$. That's not the same thing. Let me put this differently: For $f(x,y) = |x-y|$, you have $\lim_{x\to y} f(x,y) \leq 0$ for all $y$. Yet there are pairs $x,y$ for which $f(x,y) > 0$, e.g. $x=1,y=0$. – fgp Mar 12 '14 at 14:25
  • You are right again, but the fact that the limit of the quotient takes his maximal values at ${1 \over \sqrt(2)}$ implies that there is not "path" on the function that has a slope greater than $\sqrt{{2\over e}}$ because otherwise we would have found another point with greater slope on the function f. – Bman72 Mar 12 '14 at 14:30
  • 1
    Oh, and BTW, you mixed up the signs in the line "Now you notice that.... First, $f'(\frac{1}{\sqrt{2}})$ should be negative, and $f'(-\frac{1}{\sqrt{2}})$ should be positive (as per your plot ;-)). And second, the $<$ in $-\sqrt{\frac{2}{e}} < -1$ should be a $>$... – fgp Mar 12 '14 at 14:32
  • Again, no. The slope is a local property - it's the slope at one particular point. The differential quotient allows arbitrary pairs of $x$ and $y$. You have to bridge that gap somehow. I don't really know what you mean by "path on the function", but I assume you mean that geometric intuition tells you that the derivative does, indeed, bound the slope of arbitrary lines drawn between two points on the function's graph. Which is indeed true, but geometric intuition doesn't constitute a proof! – fgp Mar 12 '14 at 15:09
  • @fgp Look here at example 4.1.1 what I mean ;) – Bman72 Mar 12 '14 at 21:14
  • 1
    Exactly. That example 4.1.1 proves what you have simply assumed without stating it explictily. That was what I criticized - not that your answer was wrong (it isn't), but that it was incomplete. BTW, I'm going to edit your answer and put the proof in there, instead of referencing it - it's only a few lines.... – fgp Mar 12 '14 at 23:06
  • How does the inequality arise in the mean values thereom statement, the one with z – Sridhar Thiagarajan Jun 27 '16 at 07:08