I want to find the equation of one curve in $X-Y$ plan which satisfies the functions as follows:
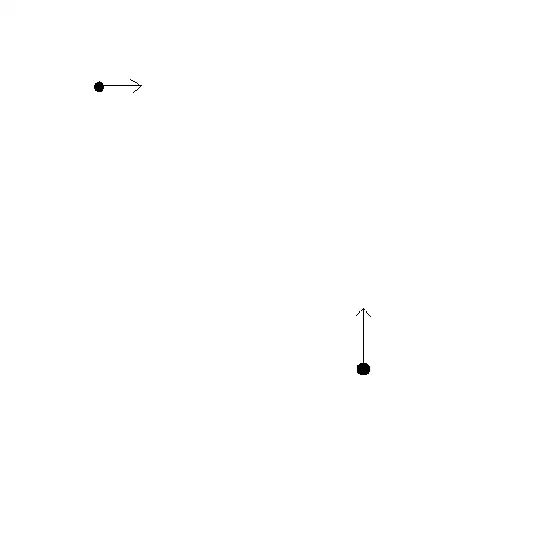
1) $A(x_1,y_1)$, $B(x_2,y_2)$ are two known points and $f(x,y)$ (or $y(x)$) is the equation of the curve we want to find;
2) $f(x,y)$ pass A and B;
3) the tangent vector of $f$ at A is $v_A=(v_{ax},v_{ay})$ and at B is $v_B=(v_{bx},v_{by})$, and $||v_A||=||v_B||=1$.
I think that there is a group of curves which satisfy these conditions, so I want to add one more condition:
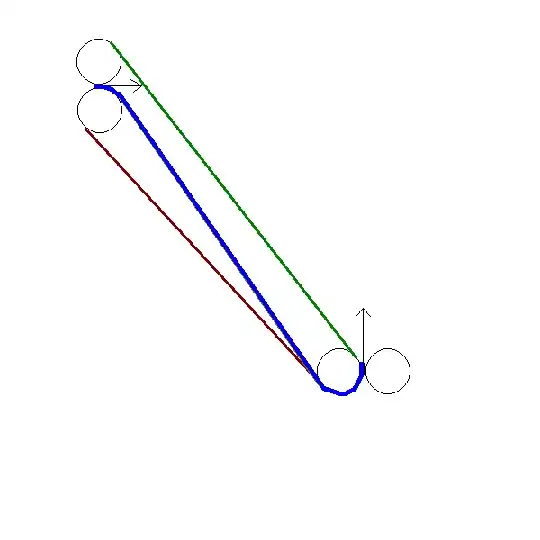
4) the length of $f $ from A to B or from B to A is the minimum.
Now how many curves are there? and how to get the equations? If you want, you can answer with a numercial example. For example, $A=(0,0),B=(1,2),f'(A)=(-1,0),f'(B)=(0,1)$.
This problem stops my work a long time, so thanks for your help.