Let $\Omega \subset \mathbb{R}^3$ be a domain. Is it true that if $H_1(\Omega)$ = 0, then $\pi_1(\Omega) = 0$? For a counterexample, the group $\pi_1(\Omega)$ needs to be a perfect group and so I was trying with the smallest one i.e. $A_5$. But I don't think the standard construction of the space from CW complexes, embeds into $\mathbb{R}^3$.
Asked
Active
Viewed 1,044 times
6
-
If you search a bit you will see that something awfully related to this has been asked here and on MO ages ago (with no conclusive answer, btw) – Mariano Suárez-Álvarez Feb 17 '14 at 19:41
-
1Here is one from MO that seems to have an answer. – John Habert Feb 17 '14 at 19:42
-
@JohnHabert: No, that MO post does not answer this question since here the question is about domains in 3d space. – Moishe Kohan Feb 17 '14 at 20:24
-
@studiosus It has been a while since I studied topology but I believe the second answer there should embed into 3-space. – John Habert Feb 17 '14 at 20:36
2 Answers
7
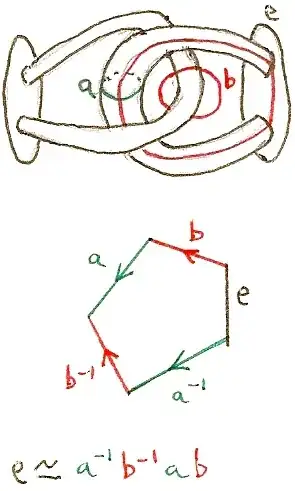
The exterior of the Alexander Horned sphere (Hatcher p.171-172) has $H_1=0$ but $\pi_1\neq 0$. (This is what Hatcher refers to as $\mathbb{R}^3\smallsetminus B$.)
Below is a diagram I made to help with Hatcher's computation of $\pi_1$ of the horned sphere. You'll find a fuller explanation in my Hatcher notes, at diagonalargument.com.
Hatcher remarks, about the computation:
In particular we see explicitly why $\pi_1(\mathbb{R}^3−B)$ has trivial abelianization, because each of its generators is exactly equal to the commutator of two other generators. This inductive construction in which each generator of a free group is decreed to be the commutator of two new generators is perhaps the simplest way of building a nontrivial group with trivial abelianization, and for the construction to have such a nice geometric interpretation is something to marvel at.
Michael Weiss
- 9,212
-
Your welcome. I've posted a follow-up question, whether there's an example like this but with $\pi_1$ finite. – Michael Weiss Feb 18 '14 at 16:34
-
-
This is an immediate consequence of Prop. 2B.1 of Hatcher (p.169). Alternately, Hatcher points out on p.172 that $\pi_1$ has trivial abelianization, and the abelianization of $\pi_1$ is $H_1$ (Theorem 2A.1, p.166). – Michael Weiss Apr 28 '17 at 17:10
2
First, suppose that you have a compact connected submanifold $C$ with nonempty boundary in 3d sphere. If some boundary components are spheres, you add the 3-ball which they bound $C$ without changing 1st homology or fundamental group. Suppose the result, which I will still call $C$, still has nonempty boundary. Recall that $$ \chi(C)=\chi(\partial C)/2, $$ Which immediately implies that the 1st Betti number of $C$ is positive. Hence, we are done in this case. The remaining possibility is that the original $C$ was simply connected to begin with.
This answers your question positively in the case of domains which are interiors of compact manifolds with boundary.
However, for general domains the answer is negative. Take a doubly wild arc in 3d space, meaning that it is wild at both ends. Then the complement is in general not simply connected but is acyclic.
Moishe Kohan
- 111,854