I am taking a first course in topology, and I am struggling with simplicial complexes. Specifically the triangulation of subspaces of $ \mathbb{R}^n $ confuses me. If you could help me on the following points I would be very grateful.
In general how do you construct a triangulation of a subspace? I have been given a very basic example, where the 2-sphere is triangulated, but how do we go about doing this for more complicated subspaces, such as the "Dunce hat" space? Additionally how do we prove or disprove the existence of such a triangulation?
Do you have any book recommendations which would help with triangulation specifically and with simplicial complexes in general?
EDIT: drew a picture for barycentric subdivison, but drawing it took ages. will find an easier way for the next one.
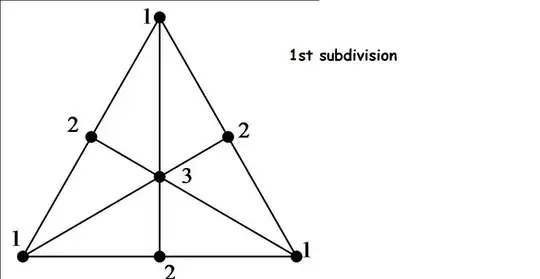
Clearly this does not give a simplicial complex. I can see how the next subdivison does.