At a fixed point $p$ of hyperbolic $n$-space $H$, there is the exponential map from flat $n$-space to $H$ taking straight lines through the origin of the flat space to hyperbolic lines through $p$ in hyperbolic space.
If $L$ is a hyperbolic line not passing through $p$, what does its preimage in the flat space look like?
First consider the case $n = 2$. View the hyperbolic plane $H$ as the isometrically embedded upper nappe of the unit hyperboloid in the Minkowski space $\mathbf{R}^{2,1}$: $$ H = \{(x, y, z) : x^2 + y^2 - z^2 = -1, z > 0\}. $$ For simplicity, assume $p = (0, 0, 1)$. The exponential map at $p$ is easily checked to be $$ (r\cos\theta, r\sin\theta) \mapsto (\sinh r \cos\theta, \sinh r \sin\theta, \cosh r). $$ In this model, a hyperbolic line $\ell$ is the intersection of $H$ with the (Minkowski-)orthogonal complement of a spacelike vector (a real plane). Up to rotation about the $z$-axis, this plane has equation $ax - cz = 0$, with $0 < c < a$, and in polar coordinates in $T_p H$, $\ell$ has equation $$ a\sinh r \cos\theta = c\cosh r $$ or, as a polar graph, $$ r = \frac{1}{2} \log \frac{\frac{a}{c} \cos\theta + 1}{\frac{a}{c} \cos\theta - 1}. $$ (This description of $H$ follows Patrick Ryan's Euclidean and Non-Euclidean Geometry. The hyperboloid model is surprisingly amenable to calculations of this type, not that the question can't be answered in the Poincaré disk model as well.)
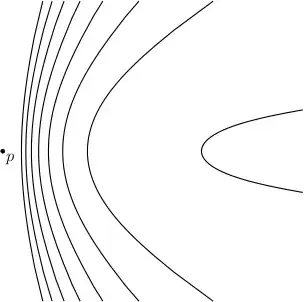
Since a (hyperbolic) line and a point lie in a (hyperbolic) plane, and since the preceding geometric assumptions can be accomplished by hyperbolic isometries, the above description is essentially general.
