For a normal random variable with mean 0.3 and standard deviation 0.03, its PDF would be as follows (I used MATLAB to draw it):
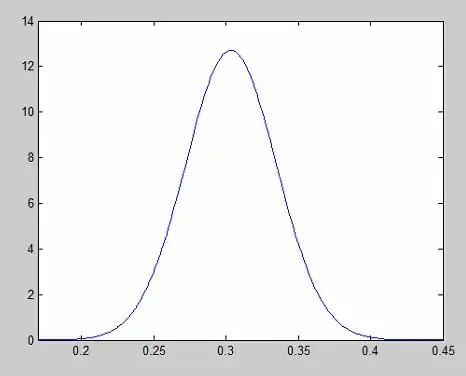
My first question is that why these probabilities are larger than 1? for example $P(X=0.3)=13.3$? should
But when I draw its CDF,all the probabilities are between 0 and 1!

Why PDF values are greater than one but CDF values are not? Thanks for your help.